Изменение направления относительной скорости точки вследствие вращательного переносного движения.
Например, если человек идет равномерно вдоль радиуса равномерно вращающейся платформы, то относительной скоростью является скорость его движения вдоль радиуса, а переносной – скорость той точки платформы, где он находится в данный момент времени (рис. 2.46).
Пусть в момент времени t человек занимает на платформе положение, показанное на рис. 2.46,а, а в момент времени t + ∆t положение, показанное на рис. 2.46,б.
Так как относительное движение равномерное и прямолинейное, то относительное ускорение человека ar = 0. Однако за время ∆t относительная скорость изменяется по направлению, вследствие вращения подвижной системы отсчёта, закрепленной на платформе.
За время ∆t происходит изменение модуля переносной скорости от Ve = I 
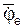I·r до Ve = I 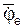I·R вследствие относительного перемещения человека. Указанные изменения относительной Vr и переносной Ve скоростей и вызывают появление кориолисова ускорения.
Модуль кориолисова ускорения определится как модуль векторного произведения:
ac = 2·ωe·Vr·sin( 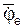,Vr),
где ωe = I 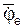I – модуль вектора угловой скорости переносного вращения.
Кориолисово ускорение равно нулю в трёх случаях:
1) если ωe = 0, т. е. в случае поступательного переносного движения или в момент обращения в нуль угловой скорости непоступательного переносного движения;
2) если Vr = 0, т. е. в случае относительного покоя точки или в момент равенства нулю модуля относительной скорости движущейся точки;
3) если sin( 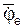,Vr) = 0, т. е. в случае, когда вектор относительной скорости Vr и вектор переносной угловой скорости 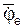параллельны (Vr || ).
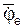Направление кориолисова ускорения определяется по правилу векторного произведения. ac ┴ Vr, ac ┴ 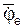и направлено в сторону, откуда поворот вектора 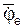к вектору Vr для совмещения их направлений виден происходящим против хода часовой стрелки. Поворот осуществляется на угол меньше 180о.
Пример. Пусть векторы 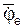и Vr лежат в горизонтальной плоскости и направлены так же, как и единичные векторы i, j правой системы отсчёта (рис. 2.47).
По правилу векторного произведения вектор ac ускорения Кориолиса направлен по отношению к векторам 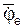и Vr так же, как и единичный вектор k по отношению к векторам i и j.
Для определения направления кориолисова ускорения используется правило Жуковского: для определения направления ускорения Кориолиса необходимо относительную скорость Vr точки спроецировать на плоскость, перпендикулярную оси переносного вращения, и повернуть эту проекцию в той же плоскости на угол 90о в сторону переносного вращения.
Для иллюстрации правила Жуковского рассмотрим движение точки по образующей конуса с относительной скоростью Vr под углом α от его вершины к основанию (рис. 2.48).
Модуль кориолисова ускорения равен
ac = 2·ωe·Vr·sin(180о – α),
где ωe – модуль вектора угловой скорости 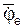переносного вращения.
На рис. 2.48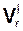 
– проекция относительной скорости Vr на плоскость (плоскость на рисунке заштрихована), перпендикулярную оси переносного вращения. Направление ускорения Кориолиса ac совпадает с направлением единичного вектора i1 неподвижной системы отсчёта O1X1Y1Z1.
Для закрепления теоретического материала необходимо выполнить курсовое задание К 4.
Варианты курсового задания К 4
«Определение абсолютной скорости
и абсолютного ускорения точки»
По заданным уравнениям относительного движения точки М и движения тела D определить для момента времени t1 абсолютные скорость и ускорение точки М. Схемы механизмов показаны на рисунках, а необходимые для расчёта данные приведены в табл. 2.4.
Определить кинематические характеристики точки М в момент времени t1 (OM(t1) – положение точки на траектории относительного движения; Ve(t1) – переносная скорость; Vr(t1) – относительная скорость; V(t1) – абсолютная скорость; ar(t1) – относительное ускорение; aе(t1) – переносное ускорение; aс(t1) – ускорение Кориолиса; a(t1) – абсолютное ускорение).
Для каждого варианта положение точки М на расчётной схеме соответствует положительному значению дуговой координаты ОМ = f(t).
Таблица 2.4
| Номер варианта | Расчётная схема механизма | Исходные данные для расчёта |
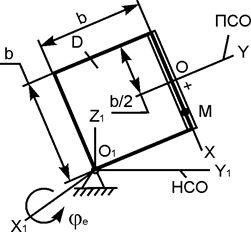
| ОМ = 18·sin(p·t/4), см; φe = 2·t3 – t2, рад; b = 25 см; t1 = 2/3 c |
Продолжение табл. 2.4
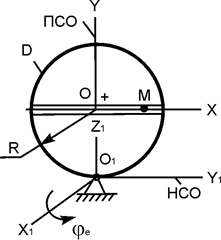
| ОМ = 20·sin(p·t), см; φe = 0,4·t2 + t, рад; R = 20 см; t1 = 5/3 c | |
| ОМ = 6·t3, см; φe = 2·t + 0,5·t2, рад; b = 30 см; t1 = 2 c | |
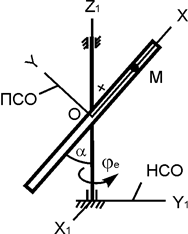
| ОМ = 10·sin(p·t/6), см; φe = 0,6·t2, рад; α = 30o; t1 = 1 c |
Продолжение табл. 2.4
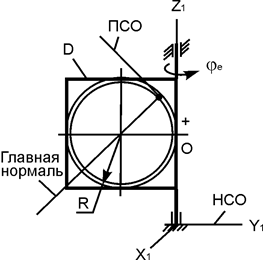
| ОМ = 40·p·сos(p·t/6), см; φe = 3·t – 0,5·t3, рад; R = 30 см; t1 = 2 c | |
| ОМ = 6·t2, см; φe = 2·t + 4·t2, рад; b = 30 см; t1 = 1 c | |
| ОМ = 20·p·сos(2·p·t), см; φe = 0,5·t2, рад; b = 40 см; α = 60o; t1 = 3/8 c |
Продолжение табл. 2.4
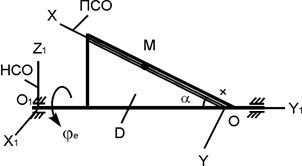
| ОМ = 6·(t + 0,5·t2), см; φe = t3 – 5·t, рад; b = 40 см; α = 30o; t1 = 2 c | |
| ОМ = 10·(1+sin(2·p·t)), см; φe = 4t + 1,6t2, рад; t1 = 1/8 c | |
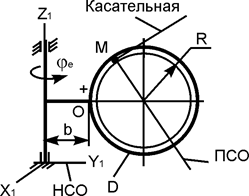
| ОМ = 20·p·сos(p·t/4), см; φe = 1,2·t – t2, рад; R = 20 см; b = 20 см; t1 = 4/3 c | |
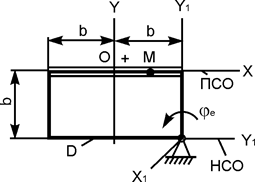
| ОМ = 20·sin(p·t/3), см; φe = 2·t2 – 0,5·t, рад; b = 25 см; t1 = 4 c |
Продолжение табл. 2.4
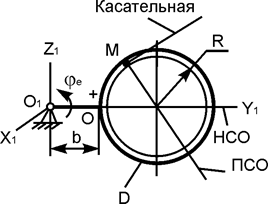
| ОМ = 15·p·t3/8, см; φe = 5·t – 4·t2, рад; R = 30 см; b = 30 см; t1 = 2 c | |
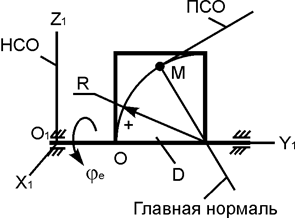
| ОМ = 120·p·t2, см; φe = 8·t2 – 3·t, рад; R = 40 см; t1 = 1/3 c | |
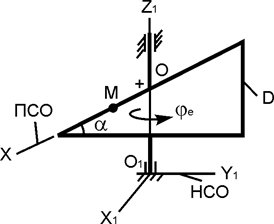
| ОМ =3+14·sin(p·t), см; φe = 4·t – 2·t2, рад; α = 30o; t1 = 2/3 c |
Продолжение табл. 2.4
|
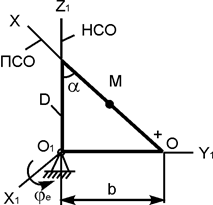
ОМ = 5· 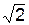 ·(t2 + t), см;
φe = 0,2·t3 + t; рад;
t1 = 2 c;
b = 60 см;
α = 45o
| |
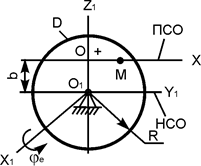
| ОМ = 20·sin(p·t), см; φe = t – 0,5·t2, рад; b = 20 см; t1 = 1/3 c | |
|
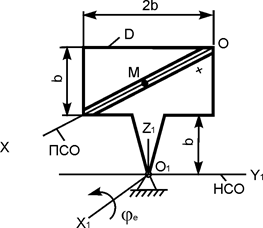
ОМ = 8·t3 + 2·t, см;
φe = 0,5·t2, рад;
b = 4· 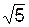 см;
t1 = 1 c
| |
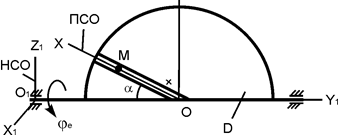
| ОМ = 10t + t3, см; φe = 8t – t2, рад; α= 30o; t1 = 2 c |
Продолжение табл. 2.4
| ОМ = 6·t + 4·t3, см; φe = t + 3·t2, рад; R = 40 см; t1 = 2 c | |
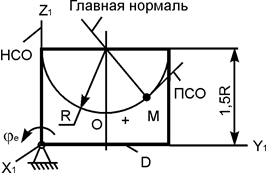
| ОМ = 30·p·cos(p·t/8), см; φe = 6·t + t2, рад; R = 60 см; t1 = 2 c | |
| ОМ = 25·(t + t2), см; φe = 2·t – 4·t2, рад; R = 25 см; t1 = 1/2 c | |
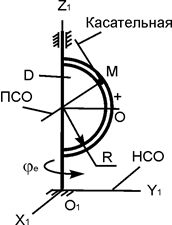
| ОМ = 10·p·sin(p·t/4), см; φe = 4·t – 0,2·t2, рад; R = 30 см; t1 = 2/3 c |
Продолжение табл. 2.4
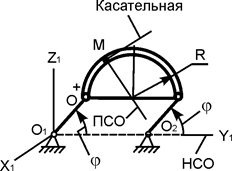
| ОМ = 6·p·t2, см; φ = p·t3/6, рад; R = 18 см; OO1 =20 см; t1 = 1 c | |
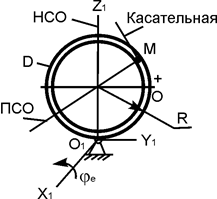
| ОМ = 75·p (0,1·t2), см; φe = 2·t – 0,3·t2, рад; R = 30 см; t1 = 1 c | |
| ОМ = 15·sin(p·t/3), см; φe = 10·t – 0,1·t2, рад; t1 = 5 c | |
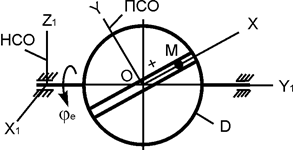
| ОМ = 8·cos(p·t/3), см; φe = 2·p·t2, рад; α = 45o; t1 = 3/2 c |
Окончание табл. 2.4
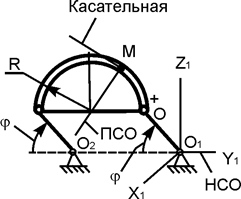
| ОМ = 6·p·t2, см; φ = p·t2/6, рад; R = 20 см; OO1 =20 см; t1 = 1 c | |
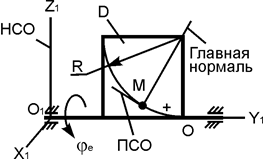
| ОМ = 2,5·p·t2, см; φe = 2·t3 – 5·t, рад; R = 40 см; t1 = 2 c | |
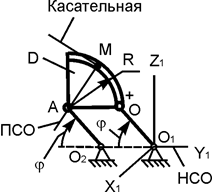
| ОМ = 6·p·t, см; φ = p·t/6, рад; R = 20 см; OO1 =20 см; t1 = 1 c | |
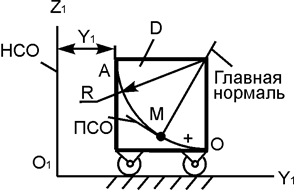
| ОМ = 4·p·t2, см; Y1= t3 + 4·t; R = 48 см; t1 = 2 c |
Дата добавления: 2015-05-30; просмотров: 1151;