Пример выполнения курсового задания К 4
Дано: уравнение относительного движения точки М
OM = Sr = Sr(t) = 2,5·p·t2, см;
уравнение вращательного движения тела D
φe = φe(t) = 2·t3 – 5·t, рад;
t1 = 1 c; R = 40 см.

Точка М движется по телу D. По заданным уравнениям относительного движения точки М и движения тела D определить для заданного момента времени t1 абсолютную скорость и абсолютное ускорение точки М (OM(t1) = ? Vr(t1) = ? Ve(t1) = ? V(t1) = ? ar(t1) = ? ae(t1) = ? ac(t1) = ? a(t1)= ?) (рис. 2.49).
Решение. Точка М осуществляет сложное движение, поэтому для решения задачи необходимо ввести неподвижную систему отсчёта O1X1Y1Z1 и подвижную систему отсчёта OXYZ. Изобразим рассматриваемый механизм в момент времени t1 (рис. 2.50).
Координатную ось O1Y1 неподвижной системы отсчёта направим по оси вращения тела D. Подвижную систему отсчёта OXYZ закрепим на теле D, расположив начало отсчёта в точке О. По исходным данным уравнение относительного движения точки М задано естественным способом Sr(t) = 2,5·p·t2. Исходя из этого, известны следующие характеристики движения: вид траектории движения – дуга окружности радиусом R; начало отсчёта дуговой координаты Sr – точка О; положительное направление отсчёта дуговой координаты Sr – знак (+); уравнение движения Sr = 2,5·p·t2.

Определим положение точки М на траектории относительного движения в момент времени t1:
Sr(t1) = 2·p·(t1)2 = 2,5·p·22 = 10p см > 0.
Для координации точки М на траектории относительного движения целесообразно использовать центральный угол:
a(t1) = Sr(t1)/R = 2,5·p·(t1)2/R = 2,5·p·22/40 = p/4.
Итак, α(t1) = 45о. Точка М тела D, совершающего вращательное движение в неподвижной системе отсчёта O1X1Y1Z1, описывает окружность радиусом
MK = R – R·cos(α(t1)) = R·(1 – cos(α(t1))= 40·(1 – 0,707) = 11,72 см.
Таким образом, траектория переносного движения точки М установлена. Это окружность радиусом МК с центром в точке К, расположенной на оси вращения тела D.
Абсолютное движение точки М – это сумма относительного и переносного движений. Таким образом, траектория абсолютного движения точки М представляет собой винтовую линию, расположенную на сферическом конусе.
Для определения абсолютной скорости V точки М используется векторное равенство
V = Vr + Ve,
где Vr – вектор относительной скорости; Ve – вектор переносной скорости.
Определим проекцию 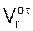 относительной скорости Vr на касательную:
относительной скорости Vr на касательную:
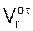 =
= 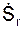 = 5·p·t.
= 5·p·t.
В момент времени t1 имеем
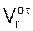 (t1) =
(t1) = 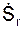 (t1) = 5·p·t1 = 5·p·2 = 10·p = 31,4 см/c > 0.
(t1) = 5·p·t1 = 5·p·2 = 10·p = 31,4 см/c > 0.
Поскольку 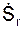 (t1) > 0, то модуль относительной Vr(t1) =
(t1) > 0, то модуль относительной Vr(t1) = 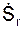 (t1), а вектор относительной скорости Vr направлен так же, как и единичный вектор τ естественной координатной системы отсчёта. Покажем этот вектор на рис. 2.50.
(t1), а вектор относительной скорости Vr направлен так же, как и единичный вектор τ естественной координатной системы отсчёта. Покажем этот вектор на рис. 2.50.
Для определения переносной скорости Ve предварительно найдем модуль ωе угловой скорости 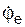 переносного вращения.
переносного вращения.
ωe = I 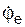 I = I6·t2 – 5I.
I = I6·t2 – 5I.
В момент времени (t1) имеем
ωe(t1) = I6·(t1)2 – 5I = I6·22 – 5I = 19 рад/c > 0.
Поскольку ωe(t1) > 0, то величина угла φе возрастает. Покажем на рис. 2.50 направление вращения и определим модуль переносной скорости Ve(t1) по формуле
Ve(t1) = ωe(t1)·МК = 19·11,72 = 222,68 см/с.
Так как Ve(t1) направлена по касательной к траектории переносного движения, то она перпендикулярна плоскости OYZ подвижной системы отсчёта. С другой стороны, Vr ┴ Ve. Исходя из этого, определим модуль абсолютной скорости:
V(t1) = 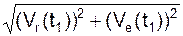 =
= 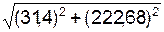 = 224,88 см/с.
= 224,88 см/с.
Если Vr не перпендикулярна Ve, то определение модуля скорости V следует определять через проекции векторного выражения V = Vr + Ve на координатные оси неподвижной системы отсчёта O1X1Y1Z1.
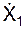 = Ve;
= Ve;  = – Vr·cos(α);
= – Vr·cos(α); 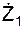 = Vr·sin(α),
= Vr·sin(α),
где 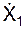 ,
,  ,
, 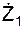 – проекции абсолютной скорости на оси O1X1, O1Y1, O1Z1 системы отсчёта O1X1Y1Z1.
– проекции абсолютной скорости на оси O1X1, O1Y1, O1Z1 системы отсчёта O1X1Y1Z1.
V(t1) = 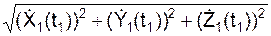 =
=
= 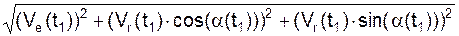 =
=
= 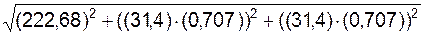 = 224,88 см/с.
= 224,88 см/с.
Для ориентации абсолютной скорости Vв пространстве неподвижной системы отсчёта определим направляющие косинусы.
cos(V,i1) = 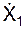 (t1)/V(t1) = 222,68/224,88 = 0,990;
(t1)/V(t1) = 222,68/224,88 = 0,990;
cos(V,j1) =  (t1)/V(t1) = (– 31,4·0,707)/224,88 = – 0,098;
(t1)/V(t1) = (– 31,4·0,707)/224,88 = – 0,098;
cos(V,k1) = 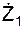 (t1)/V(t1) = (31,4·0,707)/224,88 = 0,098.
(t1)/V(t1) = (31,4·0,707)/224,88 = 0,098.
При определении абсолютного ускорения a точки М используется формула
a = ar+ ae+ ac ,
где ar – относительное ускорение; ae – переносное ускорение; ac – ускорение Кориолиса.
Поскольку относительное движение задано естественным способом, то справедливо равенство
ar= 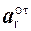 +
+ 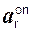 ,
,
где 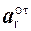 – относительное касательное ускорение;
– относительное касательное ускорение; 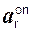 – относительное нормальное ускорение.
– относительное нормальное ускорение.
Так как переносное движение является вращательным, то переносное ускорение ae находят по формуле
ae= 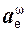 +
+ 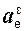 ,
,
где 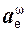 – переносное центростремительное ускорение;
– переносное центростремительное ускорение; 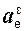 – переносное вращательное ускорение.
– переносное вращательное ускорение.
Исходную формулу для определения абсолютного ускорения можно представить в следующем виде:
a = 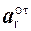 +
+ 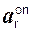 +
+ 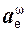 +
+ 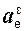 + ac.
+ ac.
Приступаем к определению слагаемых в правой части последнего выражения.
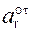 =
= 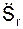 = d
= d 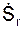 /dt = d(5·p·t)/dt = 5·p = const.
/dt = d(5·p·t)/dt = 5·p = const.
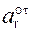 (t1) = 5·p = 5·3,14 = 15,7 см/с2 > 0 = const.
(t1) = 5·p = 5·3,14 = 15,7 см/с2 > 0 = const.
Так как 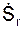 и
и 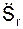 имеют одинаковые знаки, то в относительном движении точка М движется равноускоренно. Покажем вектор
имеют одинаковые знаки, то в относительном движении точка М движется равноускоренно. Покажем вектор 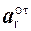 (t1) на рис. 2.50.
(t1) на рис. 2.50.
 (t1)= (Vr(t1))2/ρ = (Vr(t1))2/R = (3,14)2/40 = 24,64 см/с2 .
(t1)= (Vr(t1))2/ρ = (Vr(t1))2/R = (3,14)2/40 = 24,64 см/с2 .
Вектор 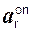 (t1)направлен по главной нормали к центру кривизны траектории относительного движения.
(t1)направлен по главной нормали к центру кривизны траектории относительного движения.
Модуль ar(t1) относительного ускорения ar(t1) в момент времени t1 определим по формуле
ar(t1) = 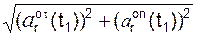 =
=
= 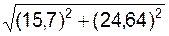 = 29,276 cм/c2.
= 29,276 cм/c2.
Модуль 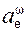 (t1) переносного центростремительного ускорения
(t1) переносного центростремительного ускорения 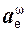 (t1) в момент времени t1 определим по формуле
(t1) в момент времени t1 определим по формуле
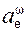 (t1) = (ωe(t1))2·MK = (19)2·11,72 = 4230,92 см/с2.
(t1) = (ωe(t1))2·MK = (19)2·11,72 = 4230,92 см/с2.
Вектор 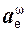 (t1) направлен к оси переносного вращения. Покажем его на рис. 2.50.
(t1) направлен к оси переносного вращения. Покажем его на рис. 2.50.
Для определения переносного вращательного ускорения 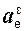 необходимо предварительно определить модуль εе переносного углового ускорения
необходимо предварительно определить модуль εе переносного углового ускорения 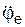 .
.
εe = I 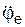 I = Id
I = Id 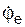 /dtI = Id(6·t2 – 5)/dtI = I12·tI.
/dtI = Id(6·t2 – 5)/dtI = I12·tI.
εe(t1) = 12·t1 = 12·2 = 24 рад/с2.
Так как 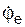 и
и 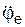 имеют одинаковые знаки, то переносное вращение происходит ускоренно. Исходя из этого, направления
имеют одинаковые знаки, то переносное вращение происходит ускоренно. Исходя из этого, направления 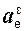 и Ve совпадают.
и Ve совпадают.
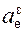 (t1) = εe(t1)·МК = 24·11,72 = 281,28 см/с2.
(t1) = εe(t1)·МК = 24·11,72 = 281,28 см/с2.
Покажем вектор 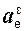 (t1) на рис. 2.50.
(t1) на рис. 2.50.
Модуль ae(t1) переносного ускорения aе(t1) в момент времени t1 определим по формуле
aе(t1) = 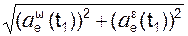 =
=
= 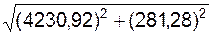 = 4240,259 cм/c2.
= 4240,259 cм/c2.
Приступаем к определению модуля ускорения Кориолиса.
ac(t1) = 2ωе(t1)·Vr(t1)·sin( 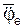 (t1), Vr(t1)).
(t1), Vr(t1)).
Согласно определению вектор 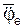 переносной угловой скорости лежит на оси вращения тела D и направлен в сторону увеличения координаты Y1 (см. рис 2.50).
переносной угловой скорости лежит на оси вращения тела D и направлен в сторону увеличения координаты Y1 (см. рис 2.50).
ac(t1) = 2ωе(t1)·Vr(t1)·sin( 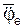 (t1), Vr(t1)) = 2ωе(t1)·Vr(t1)·sin(135o) =
(t1), Vr(t1)) = 2ωе(t1)·Vr(t1)·sin(135o) =
= 2·19·31,4·0,707 = 843,59 см/с2.
По правилу векторного произведения (ac = 2( 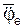 xVr)) ускорение Кориолиса ac направлено так же, как и векторы Ve и
xVr)) ускорение Кориолиса ac направлено так же, как и векторы Ve и 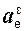 . Покажем вектор ускорения Кориолиса на рис. 2.50.
. Покажем вектор ускорения Кориолиса на рис. 2.50.
Таким образом, в векторном равенстве
a = 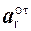 +
+ 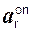 +
+ 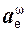 +
+ 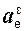 + ac
+ ac
известны все слагаемые, находящиеся в его правой части.
Определим модуль a(t1) абсолютного ускорения a(t1) через его проекции 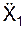 (t1),
(t1), 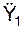 (t1),
(t1), 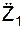 (t1) на оси неподвижной системы отсчёта O1X1Y1Z1 в момент времени (t1).
(t1) на оси неподвижной системы отсчёта O1X1Y1Z1 в момент времени (t1).
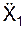 (t1) =
(t1) = 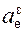 (t1) + ac(t1) = 281,28 + 843,59 = 1124,87 см/с2;
(t1) + ac(t1) = 281,28 + 843,59 = 1124,87 см/с2;
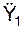 (t1) = –
(t1) = – 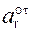 (t1)·cos(α(t1)) +
(t1)·cos(α(t1)) +  (t1)·sin(α(t1)) =
(t1)·sin(α(t1)) =
= – 15,7·0,707 + 24,64·0,707 = 6,32 см/с2;
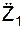 (t1) =
(t1) = 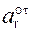 (t1)·sin(α(t1)) +
(t1)·sin(α(t1)) +  (t1)·cos(α(t1)) –
(t1)·cos(α(t1)) – 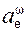 (t1) =
(t1) =
= 15,7·0,707 + 24,64·0,707 – 4230,92 = – 4202,39 см/с2;
a(t1) = 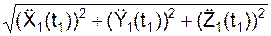 = 4350,01 см/с2.
= 4350,01 см/с2.
Для ориентации абсолютного ускорения в пространстве определим направляющие косинусы.
cos(a, i1) = 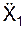 (t1)/a(t1) = 1124,87/4350,01 = 0,258;
(t1)/a(t1) = 1124,87/4350,01 = 0,258;
cos(a, j1) = 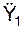 (t1)/a(t1) = 6,32/4350,01 = 0,001;
(t1)/a(t1) = 6,32/4350,01 = 0,001;
cos(a, k1) = 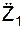 (t1)/a(t1) = – 4202,39/4350,01 = – 0,966.
(t1)/a(t1) = – 4202,39/4350,01 = – 0,966.
Результаты расчётов сводятся в таблицу.
Таблица
Кинематические характеристики точки М в момент времени t1
| Sr(t1), см | Vr(t1), см/с | Ve(t1), см/с | V(t1), см/с | 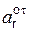 (t1),
см/с2 (t1),
см/с2
| 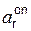 (t1),
см/с2 (t1),
см/с2
| 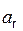 (t1),
см/с2 (t1),
см/с2
|
| 31,400 | 31,400 | 222,688 | 224,880 | 15,700 | 24,640 | 29,276 |
Окончание таблицы
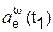 , см/с2 , см/с2
| 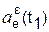 , см/с2 , см/с2
| 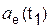 , см/с2 , см/с2
| ωe(t1), рад/с | εe(t1), рад/с2 | ac(t1), см/с2 | a(t1), см/с2 |
| 4230,920 | 281,280 | 4240,259 | 19,000 | 24,000 | 843,590 | 4350,010 |
2.28. Сферическое движение твёрдого тела
Рассмотрим движение тела, одна из точек которого во всё время движения остается неподвижной. При таком движении все остальные точки тела движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. Такое движение называют сферическим движением твёрдого тела.
Сферическое движение твёрдого тела – движение, при котором скорость одной точки тела равна нулю, а остальные точки движутся по сферическим поверхностям, центры которых совпадают с этой неподвижной точкой.
Примером сферического движения тела служит движение волчка, имеющего неподвижную точку О1 (рис. 2.51).
Для определения положения тела в каждый момент времени используют две системы отсчёта: неподвижная система отсчёта O1X1Y1Z1 и подвижная система отсчёта OXYZ, которая жёстко закреплена на теле. При этом начало отсчёта ПСО совпадает с началом отсчёта НСО.
На рис. 2.51 стрелками показаны положительные направления отсчёта углов Ψ, φ, и θ. Рассмотрим подробнее порядок отсчёта этих углов. Плоскость OXY подвижной системы отсчёта OXYZ пересекается с плоскостью O1X1Y1 неподвижной системы отсчёта O1X1Y1Z1 по линии O1L. Эту линию называют осью узлов. Введём единичный вектор р, направленный от точки О1 к точке L оси узлов. Единичные векторы i1, p лежат в горизонтальной плоскости O1X1Y1 и образуют угол Ψ, величина которого зависит от времени. Ψ = f1(t). Положительное направление отсчёта угла Ψ определяют по правилу: смотря навстречу вектору k1, поворот вектора i1 к вектору р должны увидеть происходящим против хода часовой стрелки.
Единичные векторы k1, k образуют плоскость, в которой находится угол θ, который также зависит от времени. θ = f2(t). Положительное направление отсчёта угла θ определяют по правилу: смотря навстречу вектору i, поворот вектора k1, к вектору k должны увидеть происходящим против хода часовой стрелки.
Единичные векторы р, i образуют плоскость, в которой лежит угол φ, величина которого зависти от времени. φ = f3(t). Правило положительного направления отсчёта угла φ: смотря навстречу вектору j, поворот вектора р к вектору i должны увидеть происходящим против хода часовой стрелки.

Углы Ψ, θ, φ называют также эйлеровыми углами:
угол Ψ – угол прецессии;
угол θ – угол нутации;
угол φ – угол собственного вращения.
Так как положение тела, имеющего одну неподвижную точку, определяется тремя эйлеровыми углами, т. е. тремя параметрами, то оно имеет три степени свободы.
Таким образом, сферическое движение тела описывается тремя уравнениями движения:
Ψ = f1(t); θ = f2(t); φ = f3(t).
При сферическом движении широко используют теорему Эйлера-Даламбера.
Твёрдое тело, имеющее одну неподвижную точку, можно переместить из одного положения в другое поворотом вокруг оси, проходящей через неподвижную точку (рис. 2.52).
 |
Другими словами, тело может вращаться относительно мгновенной оси вращения.
Мгновенная ось вращения – геометрическое место точек тела, скорости которых в данный момент времени равны нулю.
В случае сферического движения вектор угловой скорости Ω в данный момент времени откладывается от неподвижной точки О по мгновенной оси в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим против хода часовой стрелки.
Tело, имеющее одну неподвижную точку, можно переместить из одного положения в другое поворотом вокруг некоторой оси, проходящей через неподвижную точку. Примером такого движения является качение подвижного конуса 1 по неподвижному конусу 2 (рис. 2.53). Покажем на рисунке направление вектора мгновенной угловой скорости и запишем формулу для определения модуля скорости точки С подвижного конуса.

Так как скорость VО точки О конуса 1 равна нулю, то этот конус совершает сферическое движение. Такое движение можно представить как вращательное движение относительно мгновенной оси вращения. Мгновенная ось вращения – геометрическое место точек тела, скорости которых в данный момент времени равны нулю. Для тела 1 мгновенной осью вращения является ось ОК (см. рис. 2.53).
Вектор Ω угловой скорости тела 1 откладывается на мгновенной оси вращения в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим против хода часовой стрелки.
Модуль VC скорости точки С конуса 1 определяют по формуле
VC = Ω·CL,
где CL – кратчайшее расстояние от точки С тела 1 до мгновенной оси вращения.
Для заочной и дистанционной форм обучения выполнение контрольных работ на сферическое движение не предусмотрено. Однако такие задачи довольно часто встречаются в дидактических единицах интернет–экзамена. Приведём примеры решения задач такого типа.
Пример 1.
Подвижный конус катится по неподвижной горизонтальной плоскости O1X1Y1, имея неподвижную точку О1 (рис. 2.54).

Запишите номер вектора, по которому направлена мгновенная угловая скорость вращения.
Ответ. Мгновенная угловая скорость вращения Ω совпадает с направлением 1.
Пример 2.
Подвижный конус 1 катится без проскальзывания по неподвижному конусу 2, так, что модуль угловой скорости вращения оси О1С относительно оси О1С1 неподвижного конуса постоянен и равен ω1 рад/с (рис. 2.55).
(Для справки: sin(15o) = cos(75o) = 0,26; sin(75o) = cos(15o) = 0,96).
Мгновенная угловая скорость подвижного конуса равна …
Варианты ответов: Ω = 1,9ω1 рад/с; Ω = 2,7ω1 рад/с; Ω = 0,52ω1 рад/с; Ω = 0,35ω1 рад/с; Ω = 0,7ω1 рад/с.

Решение.
Модуль скорости точки С при вращении оси О1С относительно оси О1С1 определим по формуле VC = ω1·CM = ω1·O1C·sin(30o) (рис. 2.56).

Конус 1 вращается относительно мгновенной оси О1D вращения с угловой скоростью Ω. Исходя из этого, модуль VC скорости точки С конуса 1 равен
VC = Ω·CL = Ω·R·cos(15o) = Ω·(O1C·tg(15o))·cos(15o) =
= Ω·O1C·(sin(15o)/cos(15o))·cos(15o) = Ω·O1C·(sin(15o).
Тогда
VC = ω1·O1C·sin(30o) = Ω·O1C·(sin(15o)).
Решая последнее равенство, получим
Ω = ω1·(sin(30o)/sin(15o)) = ω1·(0,5/0,26) = 1,93 рад/с.
Правильный ответ: Ω = 1,93 рад/с.
Пример 3.
Подвижный конус 1 катится без проскальзывания по неподвижному конусу 2, так, что модуль угловой скорости вращения оси ОС относительно оси ОС1 неподвижного конуса постоянен и равен ω1 рад/с (рис. 2.57).

(Для справки: sin(15o) = cos(75o) = 0,26; sin(75o) = cos(15o) = 0,96).
Если известны углы и радиус основания R = 1 м, то мгновенная угловая скорость подвижного конуса 1 равна …
Варианты ответов: Ω = 0,73·ω1 рад/с; Ω = 0,52·ω1 рад/с; Ω = 0,28·ω1 рад/с; Ω = 1,37·ω1 рад/с; Ω = 1,92·ω1 рад/с.
Решение.
Модуль скорости точки С при вращении оси ОС относительно оси ОС1 определим по формуле VC = ω1·CM = ω1·OC·sin(75o) (рис. 2.58).

Конус 1 вращается относительно мгновенной оси О1D вращения с угловой скоростью Ω. Исходя из этого, модуль VC скорости точки С конуса 1 равен
VC = Ω·CL = Ω·(OC)·sin(45o).
Тогда
VC = ω1·OC·sin(75o) = Ω·OC·sin(75o).
Решая последнее равенство, получим
Ω = ω1·(sin(75o)/sin(45o)) = ω1·(0,96/0,707) = 1,37·ω1 рад/с.
Правильный ответ: Ω = 1,37·ω1 рад/с.
2.29. Общий случай движения твёрдого тела
 |
Рассмотрим движение свободного твёрдого тела в неподвижной системе отсчёта OXYZ (рис. 2.59).
В общем случае движение свободного тела в пространстве можно рассматривать как сумму простейших движений (три поступательных движения, параллельные координатным осям, и три вращательных движения относительно этих осей), которые осуществляются одновременно и независимо друг от друга.
Таким образом, свободное тело в пространстве имеет шесть степеней свободы.

В теоретической механике движение свободного тела в пространстве рассматривают как сложное, состоящее из поступательного движения со скоростью некоторой точки тела, принятой за полюс, и сферического движения вокруг этого полюса (рис. 2.60).
Примем произвольную точку О за полюс и поместим в него начала двух подвижных систем отсчёта OXYZ, O2X2Y2Z2. При этом система отсчёта OXYZ неподвижно закреплена на теле, а система отсчёта O2X2Y2Z2 совершает поступательное движение таким образом, что её координатные оси параллельны координатным осям неподвижной системы отсчёта O1X1Y1Z1.
Плоскости OXY, O2X2Y2 подвижных систем отсчёта пересекаются по линии OL. Введением единичного вектора р эту линию преобразуют в ось узлов.
На рис. 2.60 показаны углы Ψ, φ, θ, величины которых зависят от времени. Эти углы называют эйлеровыми углами.
Таким образом, свободное движение тела определяется шестью уравнениями движения свободного твёрдого тела.
X1О = f1(t); Y1О = f2(t); Z1О = f3(t);
Ψ = f4(t); φ = f5(t); θ = f6(t),
где X1О, Y1О, Z1О – координаты полюса О в неподвижной системе отсчёта O1X1Y1Z1.
Первые три уравнения, определяющие поступательную часть движения тела, зависят от выбора полюса О, так как координаты различных точек тела различны.
Остальные три уравнения, определяющее сферическое движение тела вокруг полюса, от выбора полюса не зависят.
 |
В технических расчётах движение свободного тела рассматривают также как вращательное движение относительно мгновенной оси вращения, проходящей через подвижный полюс (рис. 2.61).
Скорость VM любой точки М свободного тела равна геометрической сумме скорости VO полюса О и скорости VMO этой точки в её сферическом движении вокруг полюса.
VM = VO + VMO.
Скорость VMO определяют по формуле
VMO = Ω × rM,
где Ω – вектор мгновенной угловой скорости; rM – радиус-вектор, начало которого находится в полюсе, а конец в точке М.
Для студентов заочной и дистанционной форм обучения выполнение курсовых заданий на свободное движение тела не предусмотрено.
Дата добавления: 2015-05-30; просмотров: 2267;
