Пример выполнения курсового задания К 3

Дано: схема плоского механизма (рис. 2.39); модуль угловой скорости ведущего звена 1; ω₁ = ω_АО1 = 1 рад/с; геометрические параметры: АВ = О₂В = 1 м; АС = СВ = 0,5 м. Определить модули скоростей точек А, В, С и модули ω₂, ω₃ угловых скоростей звеньев АВ и ВО₂ механизма.

Решение. Согласно расчётной схеме рассматриваемый механизм состоит из трёх звеньев, обозначенных на рис. 2.39 позициями 1, 2, 3. Звено 1 (АО₁) ведущее, остальные ведомые. Звенья совершают следующие виды движений: 1 – вращательное, 2 – плоскопараллельное, 3 – вращательное.

Из условия принадлежности точки А звену 1, совершающему вращательное движение, определим модуль скорости V_A.

V_A = ω_OA·AO₁ =

= ω₁·AO₁ = ω₁·(BO₂/sin(45^о)) = 1·(1/0,707) = 1,414 м/с.

Рассмотрим отдельно плоскопараллельное движение тела 2 (рис. 2.40).

Вектор скорости V_A покажем на рис. 2.40. V_{A ┴} AO₁.

Как известно, условием безаварийной работы механизма является общая скорость в месте контакта звеньев. Исходя из этого, у звена 2 скорость точки А известна. Точка В, из условия её принадлежности звену 3, описывает окружность, поэтому линия действия скорости V_B перпендикулярна ВО₂ (V_{B ┴} BO₂).

Таким образом, у звена 2 известен вектор V_A скорости точки А и линия действия вектора V_B. Так как звено 2 совершает плоскопараллельное движение, то для определения мгновенного центра скоростей (точка Р₂) используется первый случай (см. рис. 2.33). МЦС находится на пересечении перпендикуляров к скоростям точек А и В. По направлению скорости V_A точки А определим направление вращения звена 2 относительно оси, проходящей через точку Р₂. Из условия принадлежности точки А звену 2, совершающему плоскопараллельное движение, справедливо равенство V_A = ω₂·AP₂ где ω₂ – модуль угловой скорости тела 2. Так как AP₂ = AO₁ = BO₂/sin(45^о), то V_A = ω₂·(BO₂/sin(45^о)). Из последнего равенства определим модуль ω₂ угловой скорости звена 2.

ω₂ = V_A·sin(45^о)/BO₂ = (1,414·0,707)/1 = 1,000 рад/с.

По известному модулю угловой скорости тела 2 определим модули скоростей точек В и С:

V_B = ω₂·BP₂ = 1·1 = 1, 000 м/с;

V_C = ω₂·CP₂ = ω₂· 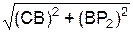= 1· = 1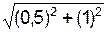, 118 м/с.

Из условия принадлежности точки В телу 3, совершающему вращательное движение, справедливо равенство V_B = ω₃·BO₂, где ω₃ – модуль угловой скорости тела 3. Из этого равенства модуль угловой скорости вращательного движения звена 3 равен

ω₃ = V_B/BO₂ = 1/1 = 1,000 рад/с.

Полученные результаты расчёта вносятся в таблицу.

Таблица

Скорости точек А, В, С показаны на рис. 2.39.

Вопросы и задания для самоконтроля

1. Сформулировать определение термина «поступательное движение твёрдого тела».

2. Записать уравнения поступательного движения тела в пространстве в декартовой системе отсчёта.

3. Записать уравнения поступательного движения тела на плоскости OXY.

4. Записать уравнения прямолинейного поступательного движения тела по горизонтали.

5. Записать выражения для определения проекций скорости центра масс на координатные оси декартовой системы отсчёта.

6. Записать выражение для определения модуля скорости центра масс тела при его поступательном движении в декартовой системе отсчёта.

7. Записать выражения для определения проекций ускорения центра масс на координатные оси декартовой системы отсчёта.

8. Записать выражение для определения модуля ускорения центра масс тела при его поступательном движении в декартовой системе отсчёта.

9. Сформулировать определение термина «вращательное движение твёрдого тела».

10. Записать уравнение вращательного движения тела.

11. Сформулировать определение термина «угловая скорость».

12. Записать формулу для определения угловой скорости вращательного движения тела.

13. Сформулировать определение термина «угловое ускорение».

14. Записать формулу для определения углового ускорения тела.

15. Записать формулу для определения модуля скорости точки при вращательном движении тела.

16. Записать формулу для определения вектора ускорения точки при вращательном движении тела.

17. Записать формулу для определения модуля центростремительного ускорения точки.

18. Записать формулу для определения модуля вращательного ускорения точки.

19. Записать формулу для определения модуля ускорения точки тела при его вращательном движении.

20. Записать уравнение равномерного вращательного движения тела.

21. Записать уравнение равнопеременного вращательного движения тела.

22. При каком сочетании угловой скорости и углового ускорения происходит ускоренное вращение тела?

24. При каком сочетании угловой скорости и углового ускорения происходит замедленное вращение тела?

25. Где прикладывают и как направляют вектор угловой скорости тела?

26. Где прикладывают и как направляют вектор углового ускорения тела при его ускоренном вращении?

27. Сформулировать определение термина «плоскопараллельное движение твёрдого тела».

28. Записать уравнения плоскопараллельного движения тела.

29. Записать формулу для определения вектора скорости точки при плоскопараллельном движении тела.

30. Сформулировать определение термина «мгновенный центр скоростей».