Скорость точки. Скорость – векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчёта.
Скорость – векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчёта.
Скорость точки всегда направлена по касательной к траектории её движения.
 Пусть заданы уравнения движения точки в пространстве: X = f1(t); Y = f2(t); Z = f3(t) (рис. 2.6).
Пусть заданы уравнения движения точки в пространстве: X = f1(t); Y = f2(t); Z = f3(t) (рис. 2.6).
Разложим вектор V скорости точки на составляющие по координатным осям: V = VOX + VOY + VOZ. Векторы VOX, VOY, VOZ называют компонентами скорости по координатным осям. Вектор Vскорости можно выразить векторным равенством:
V = i· 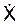 + j·
+ j· 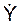 + k·
+ k·  ,
,
где 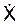 ,
, 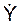 ,
, 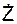 – проекции скорости V на соответствующие координатные оси.
– проекции скорости V на соответствующие координатные оси.
В инженерных расчётах рекомендуется использовать следующие обозначения проекций скорости V на координатные оси: 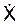 ;
; 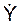 ;
;  .
.
Сравнивая последние формулы, запишем равенство
V = VOX + VOY + VOZ = i· 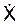 + j·
+ j· 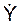 + k·
+ k·  .
.
Из этого равенства имеем:
VOX = i· 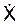 ; VOY = j·
; VOY = j· 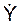 ; VOZ = k·
; VOZ = k·  .
.
Проекции скорости на координатные оси системы отсчёта равны первым производным по времени от соответствующих уравнений движения:
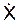 = dX/dt;
= dX/dt; 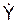 = dY/dt;
= dY/dt;  = dZ/dt,
= dZ/dt,
где точка (·) означает символ однократного дифференцирования функции по времени.
Зная проекции скорости на координатные оси, находят модуль скорости по формуле
 .
.
Ориентацию вектора скорости V в системе отсчёта OXYZ определяют по направляющим косинусам:
cos(V, i) = 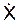 / V; cos(V, j) =
/ V; cos(V, j) = 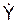 / V; cos(V, k) =
/ V; cos(V, k) =  / V.
/ V.
 Движение точки в плоскости OXY (рис. 2.7) задаётся двумя уравнениями движения: X = f1(t); Y = f2(t).
Движение точки в плоскости OXY (рис. 2.7) задаётся двумя уравнениями движения: X = f1(t); Y = f2(t).
Модуль и направление скорости точки в этом случае определяются по формулам:
 ;
;
 cos(V, i) =
cos(V, i) = 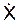 / V; cos(V, j) =
/ V; cos(V, j) = 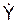 / V.
/ V.
 |
Прямолинейное движение точки (рис. 2.8) задаётся одним уравнением X = f(t).
В этом случае модуль скорости точки равен абсолютной величине проекции скорости на координатную ось ОХ.
V = | 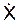 | = |dX/dt|.
| = |dX/dt|.
При 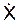 > 0 точка движется в сторону увеличения координаты Х, при
> 0 точка движется в сторону увеличения координаты Х, при 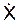 < 0 – противоположно направлению оси.
< 0 – противоположно направлению оси.
Дата добавления: 2015-05-30; просмотров: 951;
