Естественные координатные оси

Точка перемещается в пространстве по заданному уравнению движения S = f(t) (рис. 2.12).

Проведём в точке М кривой АВ соприкасающуюся плоскость, нормальную плоскость, перпендикулярную соприкасающейся плоскости, и спрямляющую плоскость, перпендикулярную соприкасающейся и нормальной плоскостям. Пересечением трёх плоскостей образован естественный трёхгранник.

Линию пересечения соприкасающейся и нормальной плоскостей называют главной нормалью.

Линию пересечения спрямляющей и соприкасающейся плоскостей называют касательной.

Линию пересечения спрямляющей и нормальной плоскостей называют бинормалью.

Естественными координатными осями называют три взаимно перпендикулярные оси: касательная (единичный вектор τ всегда направлен в сторону возрастания дуговой координаты S); главная нормаль (единичный вектор n направлен в сторону вогнутости траектории); бинормаль (единичный вектор b перпендикулярен векторам τиnи направлен так же, как и вектор k по отношению к векторам i, j в правой декартовой системе отсчёта OXYZ) (рис. 2.13).

Если в правой системе отсчёта OXYZ смотреть на единичные векторы I, jс положительного направления оси OZ (навстречу вектору k), то для совпадения направлений векторов i, j вектор iнеобходимо поворачивать против хода часовой стрелки. По такому же правилу ориентируются в пространстве векторы τ, n, b.

Начало естественных координатных осей всегда располагается в точке (см. рис. 2.12) и при движении по траектории перемещается вместе с ней. Естественные координатные оси, оставаясь взаимно перпендикулярными, изменяют своё направление в пространстве. Следовательно, естественные координатные оси образуют подвижную систему отсчёта (ПСО).

Рассмотрим движение точки на плоскости OXY (рис. 2.14).

На рис. 2.14 орты τи n расположены в соприкасающейся плоскости, а орт b не виден, так как он перпендикулярен ортам τи n и плоскости рисунка.

Главная нормаль всегда проходит через центр кривизны траектории движения точки. Здесь ρ – радиус кривизны траектории движения. При движении точки по окружности радиусом R радиус кривизны траектории ρ = R. При движении точки по прямой линии ρ = 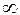. В остальных случаях при движении точки по криволинейной траектории радиус её кривизны является переменной величиной.