Ускорение точки. Ускорение а точки всегда направлено в сторону вогнутости траектории движения, лежит в соприкасающейся плоскости (см
Ускорение а точки всегда направлено в сторону вогнутости траектории движения, лежит в соприкасающейся плоскости (см. рис. 2.14) и находится по формуле
a = аoτ + аon ,
где аoτ – касательное ускорение; аon – нормальное ускорение.
Ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением, а другой направлен по касательной и называется касательным ускорением.
Касательное аoτ и нормальное аon ускорения называют также компонентами ускорения по естественным координатным осям.
Касательное ускорение аoτ характеризует быстроту изменения величины скорости V и находится по формуле
аoτ = τ·(d2S/dt2) = τ·( 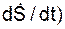 = τ·
= τ· 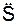 ,
,
где 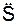 = d2S/dt2 =
= d2S/dt2 = 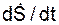 – проекция ускорения a точки на касательную.
– проекция ускорения a точки на касательную.
Таким образом, проекция ускорения точки на касательную равна второй производной по времени от дуговой координаты S = f(t) или первой производной по времени от проекции скорости на касательную.
Символ (··) означает двойное дифференцирование функции S = f(t) по времени.
Из приведённых обозначений проекций ускорения на касательную, как правило, используют обозначение 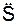 .
.
Эта проекция ( 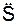 ) имеет знак (+), если направления касательного ускорения аoτ и орта τсовпадают, и знак (–), если они противоположны по направлениям.
) имеет знак (+), если направления касательного ускорения аoτ и орта τсовпадают, и знак (–), если они противоположны по направлениям.
Касательное ускорение аoτ характеризует быстроту изменения величины скорости.
Нормальное ускорение аon характеризует быстроту изменения направления скорости и находится по формуле
аon = n·( 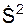 /ρ).
/ρ).
Так как 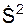 /ρ > 0, то нормальное ускорение всегда совпадает с направлением орта n, т. е. всегда направлено к центру кривизны траектории движения точки.
/ρ > 0, то нормальное ускорение всегда совпадает с направлением орта n, т. е. всегда направлено к центру кривизны траектории движения точки.
При прямолинейном движении точки радиус кривизны траектории движения ρ = 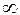 и, следовательно, аon =
и, следовательно, аon = 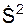 /ρ =
/ρ = 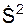 /
/ 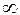 = 0.
= 0.
Таким образом, нормальное ускорение существует только при криволинейном движении.
В случае естественного способа задания движения, когда известна траектория точки, а, следовательно, её радиус кривизны ρ в любой точке и уравнение движения S = f(t), можно найти проекции ускорения точки на естественные координатные оси и по ним определить модуль и направление ускорения по формулам:
a = 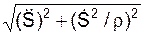 ;
;
cos(а, i) = 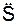 /a; cos(а, n) = (
/a; cos(а, n) = ( 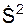 /ρ)/a.
/ρ)/a.
Модули скорости и ускорения точки при естественном и координатном способах задания движения точки связаны следующими зависимостями:
V = | 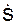 | =
| = 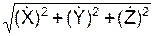 ;
;
a = 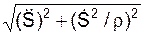 =
= 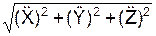 ;
;
аoτ = | 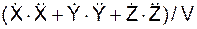 |.
|.
Дата добавления: 2015-05-30; просмотров: 945;
