Порядок решения задач с использованием принципа Даламбера.
1. Составить расчетную схему.
2. Выбрать систему координат.
3. Выяснить направление и величину ускорения.
4. условно приложить силу инерции.
5. Составить систему уравнений равновесия.
6.Определить неизвестные величины.
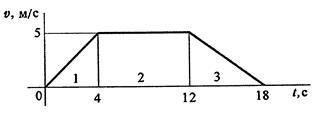Пример1. График изменения скорости лифта пи подъеме известен. Масса лифта с грузом 2800кг. Определить натяжение каната, на котором подвешен лифт на всех участках подъема
Решение:
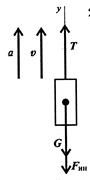
1. Рассмотрим участок 1 – подъем с ускорением. Составим схему.
Уравнение равновесия кабины лифта:
ΣFky = R1- G – F ин. = 0
R1= G + F ин.= mg+ma1R- натяжение каната, F ин.- сила инерции, растягивающая канат.
Движение на участке 1 равнопеременное, v= v0+at; v0 =0
a1= v1/t1=5/4=1,25м/ с 2.
R1= mg+ma1= m(g+a1) = 2800(9?81+1,25)= 30,97 кН.
2. Рассмотрим участок 2 – равномерный подъем.
Ускорение и сила инерции равны нулю. Натяжение каната равно силе тяжести: R2 = G = mg = 2800·9,8 = 28 кН.
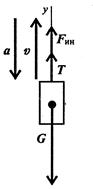
3. Участок 3 – подъем с замедлением
Ускорение направлено в сторону, обратную направлению подъема. Составим уравнение равновесия:
ΣFky = R3- G + F ин. = 0, отсюда R1 = G – F ин. = mg–ma = m(g-a3)
Ускорение(замедление) на этом участке определяется с учетом того, что v=0,
v0 + a3 ·t3 = 0; а3 = – v3/t3= –5/6 = –0,83 м/ с 2.
Натяжение каната при замедлении до остановки:
R3 = 2800(9,81–0,83) = 25144Н = 25,14 кН.
Таким образом, натяжение каната меняется при каждом подъеме и опускании, канат выходит из строя в результате усталости материала.
Пример 2.По наклонной плоскости АВ длиной 4 м и с углом подъема a = 15° равноускоренно поднимают груз М весом G = 200 кН, постоянной силой F = 65 кН, направленной параллельно наклонной плоскости. Определить, сколько времени потребуется, чтобы переместить груз на расстояние АВ, если коэффициент трения при движении груза по наклонной плоскости f = 0,05.
Решение.
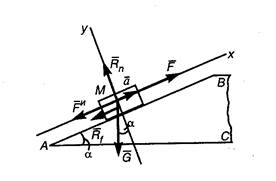
1. Находясь под действием приложенных к телу М сил G и F, а также с учетом силы трения Rf и нормальной реакции Rn, тело движется по наклонной плоскости с постоянным ускорением а.
2. Определяем время движения теля, учитывая, что оно перемещается равноускоренно без начальной скорости:
s = at2/2, откуда t = Ö2s/a
3. Так как тело движется с ускорением, то силы, приложенные к нему не образуют уравновешенной системы. Добавив силу инерции Fи =ma = Ga/g, которая направлена противоположно ускорению а, получим уравновешенную систему пяти сил G, F, Rf, Rn и Fи.
4. Получим два уравнения равновесия:
å Fkх = 0; F - G×sina - Rf - Fи = 0; (1)
å Fky = 0; Rn - G×cosa = 0; (2)
5. Из уравнения (1)
Fи = F - G×sina - Rf
сила трения
Rf = f×Rn
нормальная реакция из уравнения (2)
Rn = G×cosa
Fи = F - G×sina - fG×cosa = F - G(sina + f×cosa)
Fи = 65 - 200(sin15° + 0,05×cos15°) = 65 - 61,4 = 3,6 кН
6. Так как Fи = ma = Ga/g
найдем ускорение
a = Fи×g/G = 3,6 × 9,81 / 200 = 0,18 м/с2
7. Находим время перемещения тела М
t = Ö2s/a= Ö2 × 4 / 0,18 = 6,7 с.
Дата добавления: 2015-05-28; просмотров: 6336;