Модель доходности финансовых активов (САМР)

Модель САМР описывает зависимость между рыночным риском и требуемой доходностью при определенных условиях (инвесторы ведут себя рационально, измеряют время в одних единицах, мыслят сходным образом, заимствуют и предоставляют средства в долг под безрисковую ставку и др.). При соблюдении указанных допущений инвестиционный портфель, повторяющий пропорции рынка, должен быть оптимальным инвестиционным решением для всех инвесторов. Логика данной модели построена на том, что решение о вложении инвестиций принимается с учетом двух факторов - ожидаемой доходности 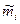и риска, мерой которого является дисперсия или стандартное отклонение доходности. Итоговое уравнение данной модели имеет следующий вид:

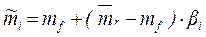, (5.11)

где 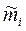- ожидаемый доход на ценную бумагу i при равновесии рынка;

m_f- ставка дохода на безрисковую ценную бумагу (например, гаранти­рованные ценные бумаги с фиксированным доходом в виде государственных облигаций).

b _i - коэффициент акции i – является мерой рыночного риска акции (измеряет изменчивость доходности акции по отношению к доходности среднерыночного портфеля). Он определяет угол наклона характеристической линии акции, построенной по статистическим данным о доходности i-й акции и среднерыночной доходности.

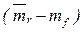– рыночная премия за риск.

Выражение (5.11) описывает линейную связь между доходом ценной бумаги и ее бета-коэффициентом и его называют уравнением линии рынка ценных бумаг (SML). Графическое изображение линии SML приведено на рис. 5.5.

Рис.5.5. Общий вид графика линии рынка ценных бумаг SML

Линия SML отражает идеальную зависимость между β и эффективностью бумаг и портфелей. Все точки, лежащие на прямой SML, соответствуют «справедливо» оцененным бумагам (портфе­лям). Над линией находится область недооцененных ценных бумаг, а под линией – область переоцененных.

Линия рынка ценных (SML) бумаг отражает зависимость риск – доходность для отдельных акций. Требуемая доходность любой акции равна безрисковой норме m_f, сложенной с произведением премии за рыночный риск 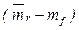и b - коэффициента акции:

Отсутствие риска по безрисковым ценным бумагам влечет за собой и мини­мальный уровень прибыли. В силу этого безрисковые бумаги являются главным регулятором прибылей и рисков.

По данным Э. Димсона (полученным на основе анализа фондовых рынков за 50 лет), в экономически развитых странах мира рыночная премия ( 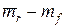) составляет 8% годовых. Например, при ставке безрискового вложения (в долларах) равной 5% годовых и коэффициенте b для некоторой компании равном 0,65, инвестор в условиях устойчивой экономики должен потребовать от акций данной компании долгосрочную доходность в размере:

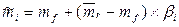= 5% + 8% x 0,65 = 10,2% годовых, долл.

Но на развивающихся рынках (в том числе и фондовый рынок России) подобные оценки могут оказаться неправомерными.

Величины коэффициентов «бета» в модели САРМив рыночной модели сходны по смыслу, но рыночная модель в отличие от САРМ не является моделью равновесия финансового рынка. Кроме того, рыночная модель использует рыночный индекс, который в общем случае не охватывает рыночный портфель, используемый в САРМ.

Существует ряд причин, по которым требуемая и ожидаемая доходности не совпадают: 1) изменение безрисковой ставки ввиду пересмотра ожидаемого темпа инфляции, 2) изменение b, 3) переоценка отношения инвеcтo-pa к риску.

Модель САРМ хорошо обоснована с позиции теории, но она не может быть подтверждена эмпирически, еепараметры с трудом поддаются оценке и поэтому ее применение на практике ограничено.

Для преодоления недостатков САРМ разработаны альтернативные модели риск – доходность. Наиболее перспективной из новых моделей построена на теории арбитражного ценообразования (Arbitrage Pricing Theory, АРТ). основы которой были сформулированы американским экономистом Жераром Дэбре, получившего Нобелевскую премию по экономике за новые подходы к общей теории экономического равновесия.