Коэффициент бета рассматривается как индекс систематического риска вследствие общих условий рынка. Осторожные инвесторы предпочитают акции с низким уровнем коэффициента бета.
Коэффициент смещения рассчитывается как разность:
a i =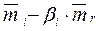 
. (5.4)
Коэффициент детерминации R2 уравнения (5.2) показывает долю рыночного риска в общем риске по данной ценной бумаге, выраженном дисперсией ее доходности.
Для определения параметров уравнения (5.2) необходимо иметь ряды наблюдений доходности отдельных ценных бумаг и ряды доходности на индекс. Такие ряды формируются по результатам котировки акций.
Биржевая котировка акций - рыночная цена акций на фондовой бирже, определяемая соотношением спроса и предложения. Котировка акций - официально публикуется и ее можно найти на различных сайтах в интернете в виде биржевых курсов акций.
Курс акции - отношение рыночной цены акции к ее номинальной, нарицательной стоимости, т.е. цена, по которой акция продается на рынке.
Доходность акции - отношение прибыли, приходящейся на одну обыкновенную акцию к ее рыночной стоимости. Доходность акций зависит от ряда факторов: темпов роста курса акции; размера выплачиваемых дивидендов; темпов инфляции и роста банковского процента; размеров налогов с прибыли. Доход по акции можно рассчитывать по ее известным курсам.
Доход по акции– представляет собой процент прибыли, которую получил бы инвестор купивший акцию в конце некоторого периода времени (дня, недели, месяца, года и др.) t-1 и продавший ее в конце следующего периода t. При этом доход может вычисляться либо в виде непрерывного сложного дохода по выражению:
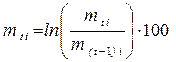, (5.5)
либо в виде дискретного дохода
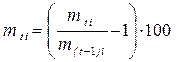. (5.6)
Здесь m t i , m (t-1)i – курсы i – ой акции в конце текущего (t) и предыдущего (t-1) периодов времени.
Если бы по акции выплачивались дивиденд, то весь доход составил бы
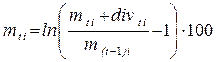, (5.7)
где div t i – дивиденд, выплачиваемый по i – ой акции на момент времени t.
Доход, подсчитанный как непрерывный сложный процент, всегда будет несколько меньше дискретного сложного процента.
При использовании выражений (5.5, 5.6 и 5.7) следует помнить, что оценка дохода такими методами возможна только в том случае, если данные о доходах в рассматриваемой выборке представляют собой распределение дохода (в вероятностном смысле) в предстоящем периоде.
Пример. 5.1.По данным инвестиционной компании «ФИНАМ» о фактической доходности акций и доходности на индекс РТС(RTSI) за период с января 2008 по май 2009 гг. (http://www.finam.ru/analysis/export/default.asp), см. табл. 5.2.
Таблица 5.2
| Индекс РТС и котировки акций на конец месяца | |||||
| Год | Месяц | RTSI | GAZP | SBER | ROSN |
| январь | 1906,97 | 290,95 | 87,89 | 172,00 | |
| февраль | 2063,94 | 304,95 | 80,2 | 196,04 | |
| март | 2053,93 | 297,61 | 73,48 | 211,21 | |
| апрель | 2122,50 | 312,49 | 77,1 | 231,20 | |
| май | 2459,88 | 360,09 | 85,2 | 286,90 | |
| июнь | 2303,34 | 341,00 | 74,29 | 272,60 | |
| июль | 1966,68 | 277,89 | 69,09 | 247,40 | |
| август | 1646,14 | 242,34 | 57,4 | 209,00 | |
| сентябрь | 1211,84 | 198,00 | 43,69 | 171,39 | |
| октябрь | 773,37 | 133,50 | 27,77 | 123,60 | |
| ноябрь | 658,14 | 118,36 | 23,21 | 108,50 | |
| декабрь | 631,89 | 107,63 | 22,79 | 110,29 | |
| январь | 535,04 | 114,70 | 16,44 | 111,16 | |
| февраль | 544,58 | 116,50 | 14,27 | 126,10 | |
| март | 689,63 | 126,40 | 20,85 | 146,59 | |
| апрель | 832,87 | 147,82 | 27,8 | 176,99 | |
| май* | 990,26 | 170,15 | 39,54 | 184,11 |
*) данные за неполный месяц
определить ожидаемую доходность, риск и параметры рыночных моделей (альфа и бета коэффициенты) для акций «Газпром»(GAZP), «Сбербанк» (SBER) и «Роснефть» (ROSN). По результатам расчета построить графики зависимостей доходности акций от доходности на индекс РТС.
Решение
1. На листе Excel вводятся среднемесячные данные по индексу РТС и котировкам акций за указанный период времени, рис.5.2, ячейки (A4:F20).
2. По выражению (5.6) рассчитываются среднемесячные значения доходностей в указанный период, пренебрегая выплатой дивидендов, рис. 5.2, ячейки (G5:J20). Среднемесячный доход по каждой акции представляет собой процент прибыли, которую получил бы инвестор, купивший акцию в конце (t-1) месяца и продавший ее в конце следующего месяца (t).
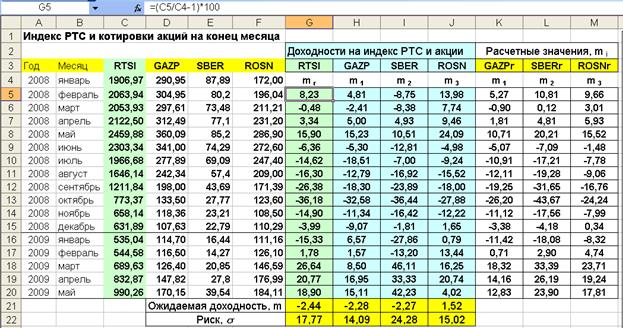
Рис.5.2. Исходные данные и результаты расчета доходностей по котировкам акций и по моделям
3. Используя статистические функции СРЗНАЧ (ячейки G21:J21), рассчитываются средние ожидаемые доходности на индекс РТС и по каждой акции. Затем с помощью функции СТАНДОТКЛОН (ячейки G22:J22) вычисляются значения риска s.
4. Воспользовавшись инструментом «Регрессия» в Пакете анализа рассчитываются параметры моделей по типу (5.2). Фрагменты из стандартного вывода результатов расчета в Excel с дополнительными комментариями приведены ниже.
По результатам расчета параметров (коэффициентов a и b) моделей, можно записать три модели связи доходностей акций с доходностью на индекс РТС:
для акций«Газпрома»m1 = - 0,56 + 0,72 mr ,
для акций«Сбербанка» m2 = 0,72 + 1,23 mr ,
для акций«Роснефть» m3 = 3,38 + 0,76 mr .
| Для акций GAZP | Для акций SBER | Для акций ROSN | |||||
| ВЫВОД ИТОГОВ | ВЫВОД ИТОГОВ | ВЫВОД ИТОГОВ | |||||
| Регрессионная статистика | Регрессионная статистика | Регрессионная статистика | |||||
| Множественный R | 0,894 | Множественный R | 0,898 | Множественный R | 0,903 | ||
| R-квадрат | 0,799 | R-квадрат | 0,806 | R-квадрат | 0,816 | ||
| Нормированный R-квадрат | 0,784 | Нормированный R-квадрат | 0,792 | Нормированный R-квадрат | 0,802 | ||
| Стандартная ошибка | 6,540 | Стандартная ошибка | 11,068 | Стандартная ошибка | 6,677 | ||
| Наблюдения | Наблюдения | Наблюдения |
| Коэффициенты для GAZP | Коэффициенты дляSBER | Коэффициенты дляROSN | |||
| Y-пересечение, a | - 0,56 | Y-пересечение, a | 0,72 | Y-пересечение, a | 3,38 |
| Переменная X1, b | 0,72 | Переменная X1, b | 1,23 | Переменная X1, b | 0,76 |
Приведенные модели могут быть использованы для прогнозной оценки ожидаемой доходности по акциям данных компаний при изменении доходности по индексу РТС. Так, например, при ожидаемой доходности на индекс РТС 2% доходность по акциям «Газпрома» составит m1 = - 0,56 + 0,72*2 = 0,88%, по акциям «Сбербанка» m2 = 0,72 + 1,23*2 = 3,18%и«Роснефть» m3 =3,38 + 0,76*2 = 4,9% , соответственно.
Как уже упоминалось выше, коэффициент детерминации R2 в полученных моделях отражает доли рыночного риска в общем риске по данной ценной бумаге. С учетом этого доля рыночного риска в общем риске наиболее полно учитывается в модели для акций ROSN поскольку для нее R2 = 0,816 и в меньшей степени в моделях для акций GAZP R2 = 0,799 и акций SBER R2 = 0,806.
5. По полученным в предыдущем пункте моделям вычисляются расчетные значения доходностей, которые затем представляются в виде линейных зависимостей доходностей соответствующих акций от доходности на индекс РТС. На этом же графике, рис.5.3 для проведения сравнения нанесены и фактические значения доходностей, выделены отдельными маркерами.
Из приведенного графика видно, что характеристики всех трех акций имеют положительный угол наклона, причем для акций Сбербанка β = 1,23 (т.е. β > 1,0) поэтому их можно отнести к агрессивным ценным бумагам, поскольку они являются более рискованными, чем рынок в целом.
Для акций Газпрома β = 0,72, он практически совпадает коэффициентом бета для акций Роснефти β = 0,76, поэтому характеристические линии имеют практически один угол наклона, т.е. они почти параллельны друг другу. Подобное расположение линий означает, что с ростом доходности фондового рынка (либо индекса рынка) РТС ожидаемая доходность всех акций возрастает, причем доходность по акциям Сбербанка растет более интенсивно, чем по акциям Газпрома и Роснефти.
В точке пересечения характеристик SBERr и ROSNr ожидаемые доходности по акциям обоих видов совпадают.
Поскольку коэффициенты смещения a i для характеристических линий двух акций (a 2, a 3) положительны, то при нулевой доходности фондового рынка (mr = 0) они обеспечат прибыль по акциям Сбербанка 0,72% и по акциям Роснефти 3,38%. Акции Газпрома имеют отрицательное значение a1= -0,56, поэтому при тех же условиях (при нулевой доходности РТС) они принесут убыток.
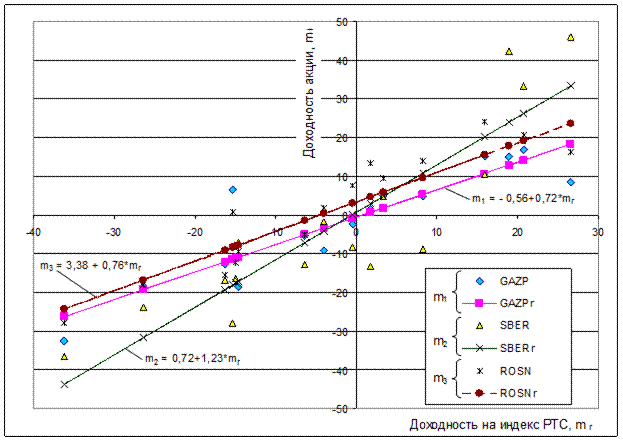
Рис.5.3. Зависимости доходности акций от доходности на индекс РТС
Дата добавления: 2015-05-28; просмотров: 1382;