Понятие точности. Постоянные ошибки

Обратимся к стандартной структуре системы автоматического управления, представленной на рис. 3.1. Основным назначением системы является как можно более точное воспроизведение управляющего сигнала. Естественно, что точность системы можно оценивать величиной разности управляющего сигнала 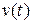и выхода 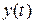, т.е. величиной ошибки 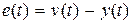. Очевидно, чем меньше величина 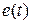пo модулю в каждый данный момент времени, тем система с большей точностью (меньшей ошибкой) воспроизводит управляющий сигнал. На практике интересуются не полной ошибкой системы 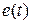, а так называемой установившейся ошибкой 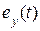, которую определяют для достаточно больших моментов времени после затухания переходной составляющей.

Изображение ошибки в соответствии с рис. 3.1 можно записать в виде

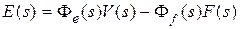, (6.1)

где , , .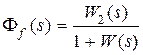

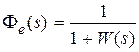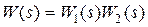Из (6.1) следует, что ошибка системы будет определяться суммой двух составляющих: ошибкой системы от управляющего и ошибкой системы от возмущающего воздействий. В силу линейности системы методика вычисления каждой из этих составляющих будет однотипной, поэтому рассмотрим лишь методы вычисления ошибки системы от управляющего сигнала.

При определенных типах воздействий и определенной структуре системы установившаяся ошибка в системе будет постоянной и может быть вычислена на основании правил операционного исчисления по выражению

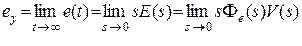. (6.2)

Рассмотрим входные воздействия: 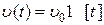, , 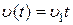, , 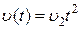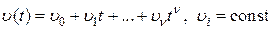изображения которых будут соответственно равны: , , , .

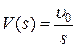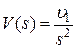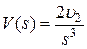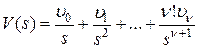Пусть передаточная функция разомкнутой системы .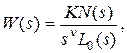

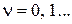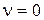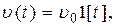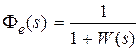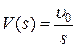Если (статическая система), то, подставляя в (6.2) и , получим

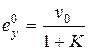. (6.3)

Ошибку 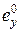будем называть статической ошибкой системы.

При 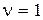(система с астатизмом первого порядка) вычислим ошибку при воздействиях 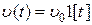и 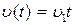. Подставляя передаточную функцию 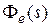и изображение входного сигнала в (6.2), получим соответственно для первого и второго типов входного сигнала

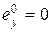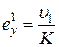, , (6.4)

где ошибку 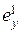будем называть ошибкой по скорости (скоростной ошибкой).

При 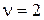и входных сигналах 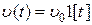, , 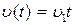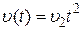соответственно получим выражения ошибок:

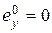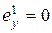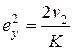, , , (6.5)

где 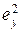– ошибка системы по ускорению.

При воздействии вида 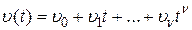для системы с астатизмом 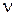-го порядка получаем

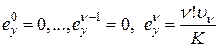. (6.6)

Из приведенных выражений следует, что ошибки в системе уменьшаются с ростом порядка астатизма системы и увеличением общего коэффициента усиления K.

На рис. 6.1 показаны переходные процессы в различных системах при отработке скачка по положению и скорости: кривая 1 – для статической системы, 2 – для системы с астатизмом первого порядка, 3 – для системы с астатизмом второго порядка.

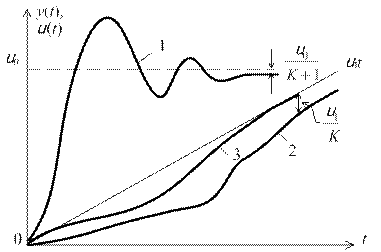
Рис. 6.1

Пример 6.1. Пусть в системе, изображенной на рис. 3.1 (см. с. 28), 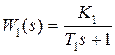, , 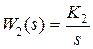, 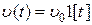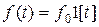. Найдем изображение сигнала ошибки, равное

.

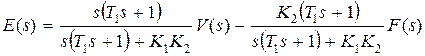Подставляя в это выражение 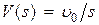и 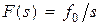и используя (6.2), получим .

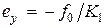Таким образом, установившаяся ошибка от управляющего воздействия равна нулю (система астатическая по отношению к управляющему сигналу), а ошибка от возмущающего воздействия постоянна (система статическая по отношению к возмущению). Для уменьшения этой ошибки следует увеличивать коэффициент усиления K₁ первого звена; величина K₂ не влияет на ошибку.

Рассмотрим ту же систему при условии, что 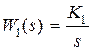, , 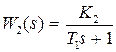т.е. интегрирующее звено находится до точки приложения возмущения. В этом случае .

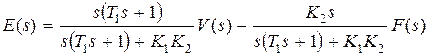Если 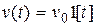, , 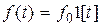то используя (6.2), получим 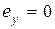, т.е. статическая ошибка как от управляющего, так и от возмущающего воздействий равна нулю и система обладает астатизмом первого порядка по отношению к обоим внешним воздействиям. Если 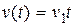, , 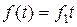то нетрудно получить 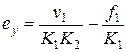, т.е. в системе имеется скоростная ошибка.

Из рассмотренных примеров следует общий вывод: система будет обладать астатизмом 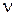-го порядка по отношению к управляющему и возмущающему сигналам, если 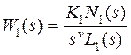, а 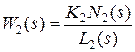. Если передаточные функции поменять местами, то система по отношению к возмущению будет статической.