Установившиеся ошибки при произвольном входном сигнале
Обозначим весовую функцию замкнутой системы по ошибке через 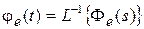 . Тогда соотношению
. Тогда соотношению 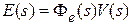 во временной области будет соответствовать свертка
во временной области будет соответствовать свертка 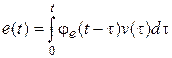 .
.
Так как нас интересует установившаяся ошибка после затухания переходной составляющей, то отнесем нижний предел интегрирования, соответствующий моменту подачи входного сигнала, в 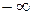 . В этом случае получим выражение, справедливое для установившегося значения сигнала ошибки:
. В этом случае получим выражение, справедливое для установившегося значения сигнала ошибки: 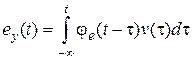 .
.
Заменив переменную интегрирования 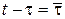 , получим
, получим
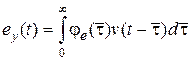 . (6.7)
. (6.7)
Полагая функцию 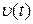 аналитической, разложим ее в ряд Тейлора при
аналитической, разложим ее в ряд Тейлора при 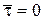 :
: 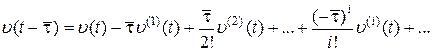 и подставим полученный ряд в (6.7). В результате получим
и подставим полученный ряд в (6.7). В результате получим
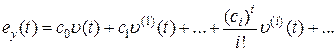 , (6.8)
, (6.8)
где коэффициенты 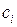 определяются выражением
определяются выражением 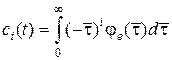 .
.
Так как передаточная функция замкнутой системы по ошибке есть прямое преобразование Лапласа от весовой функции 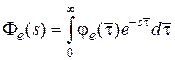 , то очевидно соотношение
, то очевидно соотношение
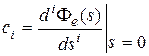 . (6.9)
. (6.9)
Коэффициенты 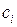 носят название коэффициентов ошибок и характеризуют, с каким весом функция
носят название коэффициентов ошибок и характеризуют, с каким весом функция 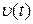 и ее производные входят в общее выражение для установившейся ошибки (6.8). Если входной сигнал изменяется достаточно медленно, то в выражении (6.8) можно ограничиться конечным числом членов ряда.
и ее производные входят в общее выражение для установившейся ошибки (6.8). Если входной сигнал изменяется достаточно медленно, то в выражении (6.8) можно ограничиться конечным числом членов ряда.
Если  , то
, то 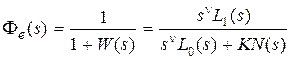 . В статической системе
. В статической системе 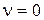 и
и 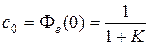 , для системы с астатизмом первого порядка имеем
, для системы с астатизмом первого порядка имеем 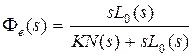 и
и 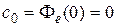 , а
, а
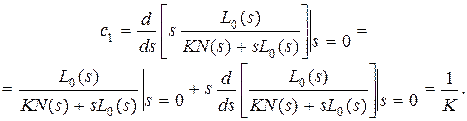
Аналогично можно показать, что для астатической системы с астатизмом 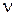 -го порядка
-го порядка  ,
, 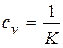 .
.
Коэффициент 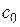 называют коэффициентом статической ошибки,
называют коэффициентом статической ошибки, 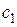 – коэффициентом скоростной ошибки,
– коэффициентом скоростной ошибки,  – коэффициентом ошибки по ускорению. Из (6.8) следует, что если
– коэффициентом ошибки по ускорению. Из (6.8) следует, что если 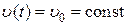 , то
, то 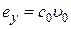 , если
, если 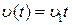 , то
, то 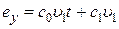 .
.
В общем случае формула (6.9) редко используется для вычисления 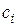 . На практике применяется другой способ. Разложим передаточную функцию
. На практике применяется другой способ. Разложим передаточную функцию 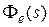 в ряд Маклорена при s = 0:
в ряд Маклорена при s = 0:
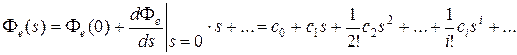 . (6.10)
. (6.10)
С другой стороны, так как 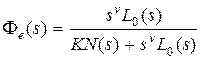 есть отношение полиномов, то деля полином числителя на полином знаменателя, получим ряд
есть отношение полиномов, то деля полином числителя на полином знаменателя, получим ряд
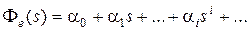 . (6.11)
. (6.11)
Приравнивая коэффициенты при одинаковых степенях s в (6.10), (6.11), получим
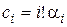 . (6.12)
. (6.12)
Величина коэффициентов ошибок в конечном итоге определяет величину ошибки в системе. Из изложенного выше вновь следует, что величины 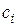 будут тем меньше, чем выше порядок астатизма системы и чем больше величина коэффициента усиления K разомкнутой системы.
будут тем меньше, чем выше порядок астатизма системы и чем больше величина коэффициента усиления K разомкнутой системы.
Пример 6.2. Пусть передаточная функция разомкнутой системы имеет вид 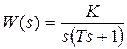 . Найдем первые три коэффициента ошибок. Передаточная функция замкнутой системы по ошибке будет равна
. Найдем первые три коэффициента ошибок. Передаточная функция замкнутой системы по ошибке будет равна 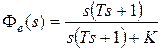 . Деля полином числителя на полином знаменателя, получим
. Деля полином числителя на полином знаменателя, получим 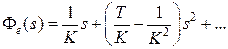 .
.
В соответствии с (6.12) найдем 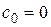 ,
, 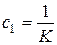 ,
, 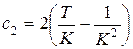 .
.
Определим установившуюся ошибку в системе при воздействии 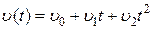 . Подставляя найденные значения
. Подставляя найденные значения 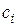 и заданные значения функции
и заданные значения функции 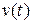 и ее производных в (6.8), получим
и ее производных в (6.8), получим  .
.
Дата добавления: 2015-05-26; просмотров: 992;
