Интегральные оценки качества
Интегральные оценки качества являются интегралами по времени от некоторых функций координат системы (выходной координаты, сигнала ошибки) и оценивают одним числом как величину отклонения, так и время регулирования. В качестве исследуемого процесса обычно выбирается разность между установившимся процессом в системе и самой координатой. Рассмотрим замкнутую систему управления стандартной структуры, на вход которой поступает единичный ступенчатый сигнал υ(t) = 1[t]. Тогда реакция системы будет представлять собой переходную функцию 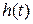 , которая в соответствии с (4.10) определяется выражением
, которая в соответствии с (4.10) определяется выражением 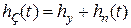 , где
, где 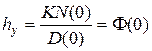 – установившаяся составляющая;
– установившаяся составляющая; 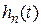 – переходная составляющая, характеризующая переходной процесс.
– переходная составляющая, характеризующая переходной процесс.
Введем отклонение 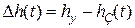 процесса
процесса 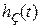 от его установившегося значения. Очевидно, что
от его установившегося значения. Очевидно, что 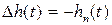 .
.
Простейшими интегральными оценками качества являются:
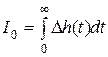 , (7.8)
, (7.8)
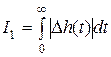 , (7.9)
, (7.9)
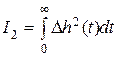 . (7.10)
. (7.10)
Оценка 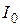 носит название линейной интегральной оценки,
носит название линейной интегральной оценки, 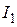 – абсолютной интегральной и
– абсолютной интегральной и 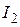 – квадратичной интегральной оценки.
– квадратичной интегральной оценки.
Значение интегралов будет конечной величиной только в том случае, если 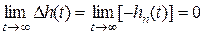 , т.е. только для асимптотически устойчивых систем.
, т.е. только для асимптотически устойчивых систем.
Поясним физический смысл оценок (7.8)–(7.10), для чего обратимся
к рис. 7.3. Для 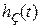 , соответствующих кривым 1, 2, 3 (см. рис. 4.2), построены графики отклонения
, соответствующих кривым 1, 2, 3 (см. рис. 4.2), построены графики отклонения 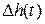 (на рис. 7.3 соответственно кривые 1, 2, 3).
(на рис. 7.3 соответственно кривые 1, 2, 3).
Величина 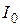 для кривой 1 есть величина площади, ограниченной этой кривой и координатными осями.
для кривой 1 есть величина площади, ограниченной этой кривой и координатными осями.
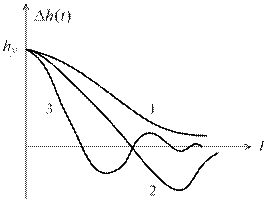 Рис. 7.3
Рис. 7.3
| Очевидно, чем меньше 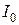 , тем меньше текущие отклонения , тем меньше текущие отклонения 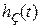 от установившегося значения и тем меньше будет время регулирования в системе. В идеальном случае, если от установившегося значения и тем меньше будет время регулирования в системе. В идеальном случае, если 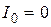 , время регулирования будет равно нулю. Для кривых 2, 3 в силу того, что они меняют свой знак, оценка , время регулирования будет равно нулю. Для кривых 2, 3 в силу того, что они меняют свой знак, оценка 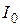 неприменима, так как величина интеграла может оказаться очень малой (даже равной нулю), но процессы будут затухать медленно. Поэтому линейные интегральные оценки можно применять, если неприменима, так как величина интеграла может оказаться очень малой (даже равной нулю), но процессы будут затухать медленно. Поэтому линейные интегральные оценки можно применять, если
|
заведомо известно, что переходная составляющая имеет монотонный характер.
Для колебательных процессов обычно применяются оценки 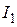 ,
, 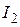 , которые имеют аналогичный смысл: чем меньше величина I, тем меньше время регулирования и меньше отклонения координаты системы от установившегося процесса.
, которые имеют аналогичный смысл: чем меньше величина I, тем меньше время регулирования и меньше отклонения координаты системы от установившегося процесса.
Любые интегральные оценки носят качественный и сравнительный характер, т.е. по величине I нельзя определить, например, время регулирования или перерегулирование в системе. Но если для двух вариантов проектируемой системы окажется, что 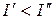 , то считается, что качественные показатели первой системы лучше, чем второй.
, то считается, что качественные показатели первой системы лучше, чем второй.
Наиболее просто вычисляются интегральные оценки 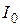 и
и 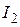 . Пусть передаточная функция замкнутой системы имеет вид
. Пусть передаточная функция замкнутой системы имеет вид
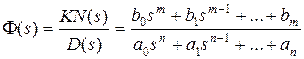 . (7.11)
. (7.11)
Найдем изображение отклонения 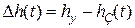 с учетом того, что
с учетом того, что 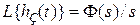 ,
, 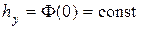 и
и 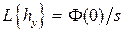 :
:
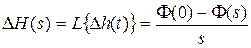 . (7.12)
. (7.12)
Так как 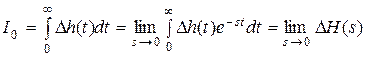 , то с учетом (7.11) имеем
, то с учетом (7.11) имеем
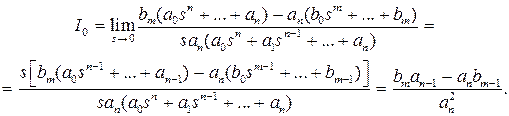
| (7.13) |
квадратичная интегральная оценка 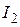 может быть определена на основе
может быть определена на основе
формулы Парсеваля (или Релея).
В частности, для астатических систем
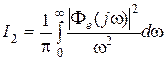 . (7.14)
. (7.14)
Изображение отклонения 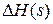 всегда можно представить как отношение двух полиномов:
всегда можно представить как отношение двух полиномов:
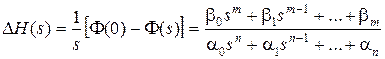 . (7.15)
. (7.15)
При этом оценка 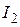 может быть аналитически вычислена при m < n через коэффициенты
может быть аналитически вычислена при m < n через коэффициенты 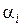 ,
, 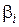 (7.15). Выражение для вычисления
(7.15). Выражение для вычисления 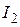 имеет достаточно сложный вид и здесь не приводится. Для наиболее распространенного случая
имеет достаточно сложный вид и здесь не приводится. Для наиболее распространенного случая
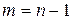 приведем несколько конечных выражений для вычисления
приведем несколько конечных выражений для вычисления 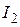 :
:
|
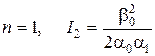 ;
; 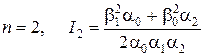 ;
;
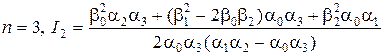 .
.
Наряду с оценками 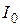 ,
, 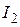 употребляются и более сложные интегральные оценки, учитывавшие не только само отклонение
употребляются и более сложные интегральные оценки, учитывавшие не только само отклонение 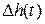 , но и его производные.
, но и его производные.
При использовании интегральных оценок можно выделить два направления: анализ системы – получение оценки для заданной системы и синтез системы – минимизация оценки по каким-либо параметрам.
Пример 7.2. Рассмотрим методику применения интегральных оценок к системе, исследуемой в примере 7.1. Передаточная функция замкнутой системы имеет вид 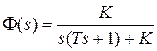 , и в соответствии с (7.11) имеем
, и в соответствии с (7.11) имеем
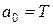 ,
, 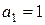 ,
, 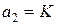 ,
, 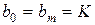 . Линейная интегральная оценка (7.13)
. Линейная интегральная оценка (7.13)
в этом случае 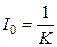 . Оценка справедлива для монотонных процессов, когда корни характеристического уравнения замкнутой системы различны, т.е. выполняется условие
. Оценка справедлива для монотонных процессов, когда корни характеристического уравнения замкнутой системы различны, т.е. выполняется условие 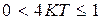 ,
, 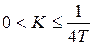 . Итак, увеличение величины K уменьшает
. Итак, увеличение величины K уменьшает 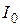 и время регулирования. Минимальное значение
и время регулирования. Минимальное значение 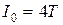 при
при 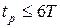 .
.
Вычислим для этой же системы величину 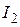 , для чего найдем изображение отклонения
, для чего найдем изображение отклонения 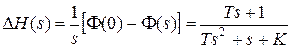 .
.
Коэффициенты в (7.15) будут 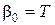 ,
, 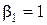 ,
, 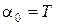 ,
, 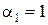 ,
, 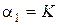 .
.
Используя (7.16), получим 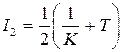 , откуда следует, что для уменьшения
, откуда следует, что для уменьшения 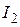 надо увеличивать величину K, либо уменьшать Т, что повышает быстродействие системы.
надо увеличивать величину K, либо уменьшать Т, что повышает быстродействие системы.
Дата добавления: 2015-05-26; просмотров: 1180;
