Корневые оценки качества. Переходная функция замкнутой системы как реакция системы на единичный скачок по положению вычисляется в соответствии с выражением (4.11)

Переходная функция замкнутой системы как реакция системы на единичный скачок по положению вычисляется в соответствии с выражением
(4.11), в котором второе слагаемое в виде суммы определяет переходную
составляющую

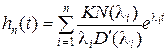, (7.1)

a 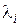– различные корни характеристического уравнения замкнутой системы .

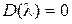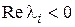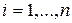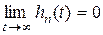Если , , то , т.е. с течением времени переходная составляющая затухает.

В выражении (7.1) перейдем к модулям в левой и правой частях:

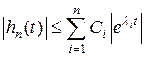, (7.2)

где .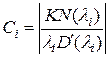

Обозначим расстояние от мнимой оси до ближайших действительного корня (рис. 7.1, а) или пары комплексно-сопряженных корней (рис. 7.1, б) на плоскости корней 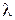через .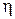

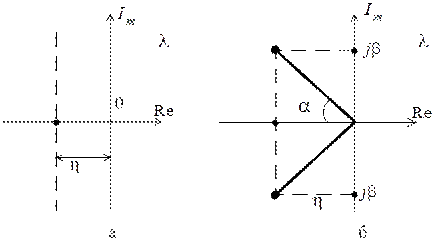
Рис. 7.1

Величину 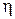будем называть степенью устойчивости. Очевидно, что 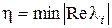. Так как 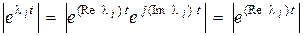, то для любого множителя 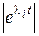в (7.2) будет справедлива оценка 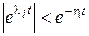. Таким образом, (7.2) равносильно выражению

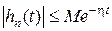, а 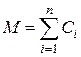. (7.3)

Из (7.3) следует, что переходная составляющая 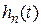затухает быстрее, чем экспонента с показателем – 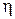. Если принять время регулирования 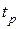как время, начиная с которого 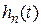войдет в 5 % трубку от начального значения, то из (7.3) получим 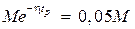, откуда

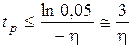. (7.4)

Выражение (7.4) и соответственно величина 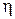характеризуют предельное быстродействие системы, поэтому иногда величину 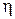называют еще мерой быстродействия системы.

Из рассмотренного выше следует, что доминирующее влияние на характер переходного процесса оказывают ближайшие к мнимой оси корни. Если ближайшими являются комплексно-сопряженные корни 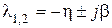, то наряду со степенью устойчивости вводят в рассмотрение колебательность системы (колебательность переходного процесса) 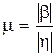. Паре комплексно-сопряженных корней в (7.1) соответствует составляющая

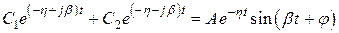, (7.5)

где 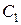, 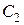– комплексно-сопряженные величины; A, 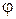– действительные величины.

Составляющая (7.5) носит колебательный характер. Период колебания определяется величиной 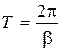. Уменьшение амплитуды в (7.5) за период Т будет равно 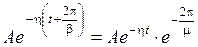, т.е. определяться величиной .

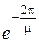Перерегулирование в % может быть оценено по формуле

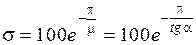. (7.6)

С увеличением 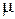увеличивается число колебаний за время регулирования и возрастает перерегулирование. Величина 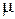носит качественный характер и является оценкой переходного процесса сверху, поэтому в действительности переходной процесс может иметь лучшие показатели.

Характер переходного процесса в значительной степени зависит от корней 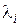характеристического уравнения, т.е. от полюсов передаточной функции 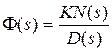замкнутой системы. Однако на величину амплитуды переходных составляющих будут влиять и нули передаточной функции. Пусть полином N(s) имеет m нулей 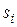, тогда 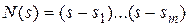и выражение (7.1) примет вид .

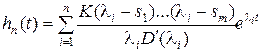Очевидно, если какой-то полюс 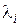будет близок (или в идеальном случае равен) нулю передаточной функции, то составляющая, соответствующая корню 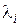, будет мала по амплитуде (или равна нулю).

Впервые корневые оценки качества переходных процессов для систем третьего порядка были предложены в работе И. А. Вышнеградского (1876), положившей начало развитию теории автоматического управления.

Характеристическое уравнение системы третьего порядка 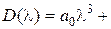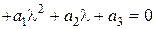путем замены переменной приводится к виду

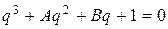, (7.7)

где , , .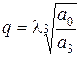

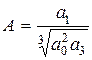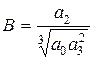Коэффициенты А, В – параметры Вышнеградского – являются комбинацией коэффициентов 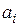и в конечном итоге зависят от реальных параметров системы. Условие асимптотической устойчивости для уравнения (7.7) несложно получить с помощью критерия Гурвица, оно имеет вид АВ > 1. В области устойчивости, ограниченной гиперболой АВ = 1 в плоскости параметров А, В,нанесем кривые, разделяющие область устойчивости на области с одинаковым расположением корней характеристического уравнения (7.7).

На рис. 7.2 представлена диаграмма Вышнеградского, где для каждой области показано расположение корней и вид переходного процесса.

Таким образом, выбирая из диаграммы требуемый вид переходного процесса, можно найти необходимые значения параметров А, В или .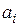

В заключение отметим ряд простых случаев, когда получены оценки степени устойчивости 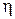и соответственно быстродействия системы. Рассмотрим систему управления стандартной структуры, изображенной на рис. 3.1. Пусть передаточная функция объекта управления 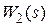имеет вид 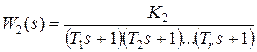, где .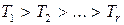

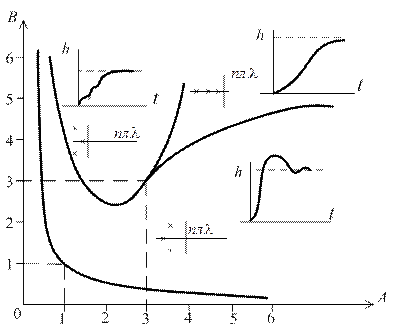
рис. 7.2

Передаточную функцию 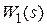будем рассматривать как передаточную функцию регулятора (управляющего устройства). Рассмотрим три случая закона управления: интегральный 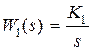, пропорциональный 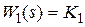, пропорционально-интегральный 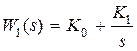. Быстродействие объекта управления может быть охарактеризовано величиной 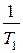. Доказано, что для интегрального закона управления быстродействие замкнутой системы, характеризуемое величиной степени устойчивости 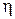, не будет превосходить быстродействия объекта, т.е. .

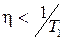Для пропорционального и пропорционально-интегрального законов управления быстродействие замкнутой системы управления может превосходить быстродействие объекта управления, но будет ограничено неравенством .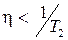

Приведенный частный результат распространяется на более общий
случай: астатические системы уступают по быстродействию системам статическим.

Пример 7.1. Пусть передаточная функция разомкнутой системы имеет вид . Характеристическое уравнение замкнутой системы 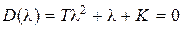имеет корни .

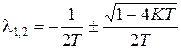Если 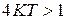, то имеем два комплексно-сопряженных корня и , , .

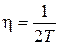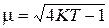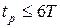Если 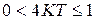, то имеем два действительных корня и , , .

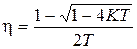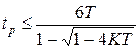Из приведенных соотношений следует, что при 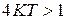процессы в системе будут носить колебательный характер, а быстродействие системы будет ограничено величиной 6Т. При 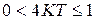процессы носят апериодический характер, но быстродействие в системе уменьшается.