Частотные оценки качества. Частотные оценки качества базируются на связи частотных и временных характеристик системы управления
Частотные оценки качества базируются на связи частотных и временных характеристик системы управления, в частности, на связи переходной функции замкнутой системы 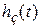 и вещественной частотной характеристики
и вещественной частотной характеристики 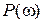 (4.13). Из (4.13) можно получить две категории оценок, одна из которых строго обоснована и математически доказана, а другая получена на основе построения большого числа переходных процессов для различных
(4.13). Из (4.13) можно получить две категории оценок, одна из которых строго обоснована и математически доказана, а другая получена на основе построения большого числа переходных процессов для различных 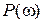 и осреднения полученных результатов.
и осреднения полученных результатов.
Рассмотрим первую группу оценок.
1. Начальное значение Р(0) и конечное значение 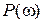 связаны с конечным значением
связаны с конечным значением 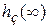 и начальным
и начальным 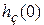 соотношениями
соотношениями
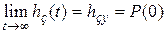 ,
, 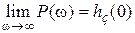 . (7.17)
. (7.17)
Эти свойства фактически являются следствием теорем о конечном и начальном значениях оригинала в преобразовании Лапласа. Так как для астатических систем 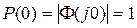 , а для статических
, а для статических 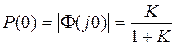 , то
, то
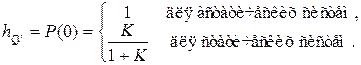
2. Сжатию характеристики 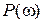 по оси
по оси 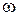 соответствует пропорциональное растяжение характеристики
соответствует пропорциональное растяжение характеристики 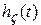 по оси t. Это свойство является следствием из свойств преобразования Фурье об изменении масштаба по оси ординат. Приведенное свойство дает важную сравнительную оценку переходных процессов в системах: более пологим характеристикам
по оси t. Это свойство является следствием из свойств преобразования Фурье об изменении масштаба по оси ординат. Приведенное свойство дает важную сравнительную оценку переходных процессов в системах: более пологим характеристикам 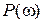 (более растянутым вдоль оси
(более растянутым вдоль оси 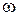 ) соответствуют более быстро протекающие переходные процессы, а более крутым или сжатым вдоль оси
) соответствуют более быстро протекающие переходные процессы, а более крутым или сжатым вдоль оси 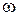 – замедленные процессы. Соответственно следует ожидать, что для первого случая время регулирования
– замедленные процессы. Соответственно следует ожидать, что для первого случая время регулирования 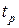 будет меньше, чем для второго.
будет меньше, чем для второго.
3. Достаточным условием того, чтобы перерегулирование 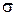 в системе не превышало 18 %, является выполнение соотношений
в системе не превышало 18 %, является выполнение соотношений
 ,
, 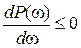 , (7.18)
, (7.18)
т.е. 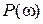 является невозрастающей положительной функцией частоты.
является невозрастающей положительной функцией частоты.
4. Достаточным условием монотонности переходного проходного процесса, т.е. 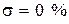 , является выполнение соотношений
, является выполнение соотношений
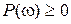 ,
, 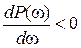 . (7.19)
. (7.19)
На рис. 7.4, а представлены две вещественные частотные характеристики, из которых для первой 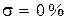 , а для второй –
, а для второй – 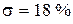 .
.
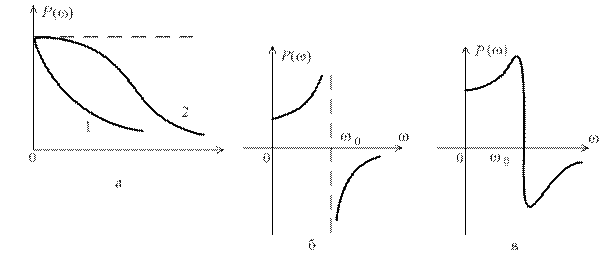
Рис. 7.4
5. Если характеристическое уравнение замкнутой системы 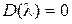 имеет чисто мнимый корень
имеет чисто мнимый корень 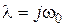 , то характеристика
, то характеристика 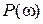 при
при 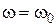 имеет разрыв непрерывности, что соответствует незатухающей гармонической составляющей с частотой
имеет разрыв непрерывности, что соответствует незатухающей гармонической составляющей с частотой 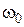 в переходном процессе
в переходном процессе 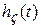 . График такой характеристики представлен на рис. 7.4, б. Поэтому если характеристика вблизи некоторой частоты
. График такой характеристики представлен на рис. 7.4, б. Поэтому если характеристика вблизи некоторой частоты 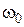 имеет резкий перепад и большие пики, то следует ожидать наличия в переходной функции медленно затухающей гармонической составляющей частоты
имеет резкий перепад и большие пики, то следует ожидать наличия в переходной функции медленно затухающей гармонической составляющей частоты 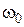 . Такой случай представлен на рис. 7.4, в.
. Такой случай представлен на рис. 7.4, в.
Оценки второй группы, как указывалось выше, имеют приближенный и в значительной степени эмпирический характер.
На рис. 7.5, а, б показаны случаи аппроксимации вещественной характеристики 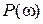 соответственно одной и суммой двух трапецеидальных характеристик.
соответственно одной и суммой двух трапецеидальных характеристик.
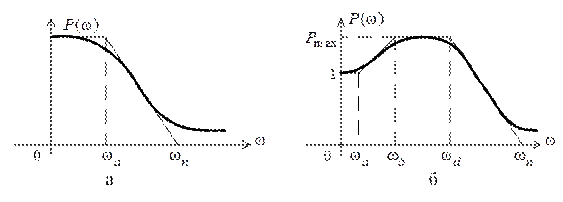
Рис. 7.5
Для случая, изображенного на рис. 7.5, а, время регулирования 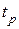 оценивается по неравенству
оценивается по неравенству
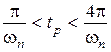 . (7.20)
. (7.20)
Для случая аппроксимации в виде суммы двух трапеций (см. рис. 7.5, б) время регулирования 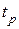 и перерегулирования
и перерегулирования 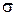 более сложным образом зависит от параметров аппроксимирующих трапеций.
более сложным образом зависит от параметров аппроксимирующих трапеций.
На рис. 7.6 представлены графики зависимостей 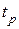 и
и 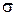 от
от 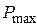 при
при 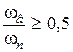 ,
, 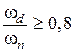 ;
; 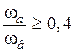 .
.
 Рис. 7.6
Рис. 7.6
| На этом рисунке время регулирования 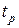 построено в относительных единицах, где построено в относительных единицах, где 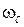 – частота среза разомкнутой системы.
Оценку (7.20) приближенно можно применять и для системы, имеющей произвольную вещественную характеристику – частота среза разомкнутой системы.
Оценку (7.20) приближенно можно применять и для системы, имеющей произвольную вещественную характеристику 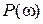 . При этом величину . При этом величину 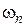 следует выбирать такой, после которой следует выбирать такой, после которой 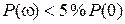 .
для характеристики рис. 7.5, б справедлива такая оценка перерегулирования: .
для характеристики рис. 7.5, б справедлива такая оценка перерегулирования:  . .
|
Наряду с оценками качества системы по переходной функции 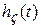 широкое распространение получили оценки качества системы при отработке гармонических входных сигналов. Особенно это касается исследования следящих систем, для которых изменяющиеся по амплитуде и знаку входные сигналы наиболее характерны. При таком подходе удобнее пользоваться АЧХ замкнутой системы
широкое распространение получили оценки качества системы при отработке гармонических входных сигналов. Особенно это касается исследования следящих систем, для которых изменяющиеся по амплитуде и знаку входные сигналы наиболее характерны. При таком подходе удобнее пользоваться АЧХ замкнутой системы 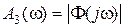 , типичный график которой представлен на рис. 7.7.
, типичный график которой представлен на рис. 7.7.
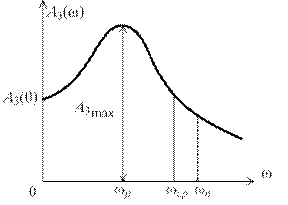 Рис. 7.7 Рис. 7.7
| Величина 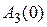 для астатических систем равна 1, а для статических для астатических систем равна 1, а для статических 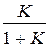 и при большом K близка к единице. Частота и при большом K близка к единице. Частота 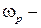 резонансная частота, при которой резонансная частота, при которой 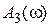 достигает максимального значения достигает максимального значения 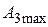 . Частота . Частота 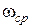 – частота среза замкнутой системы, при которой – частота среза замкнутой системы, при которой 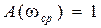 ( ( 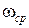 не совпадает с частотой среза разомкнутой системы, которая не совпадает с частотой среза разомкнутой системы, которая
|
обозначается 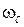 ). Интервал частот
). Интервал частот 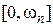 определяет полосу пропускания системы. Величина
определяет полосу пропускания системы. Величина  может задаваться из условий точности воспроизведения гармонического сигнала (см. подразд. 6.3).
может задаваться из условий точности воспроизведения гармонического сигнала (см. подразд. 6.3).
Частота 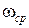 косвенно характеризует время регулирования в замкнутой системе, которое оценивается величиной
косвенно характеризует время регулирования в замкнутой системе, которое оценивается величиной 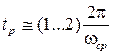 .
.
Для оценки склонности системы к колебаниям вводят так называемый показатель колебательности, который определяется как
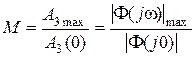 (7.21)
(7.21)
либо иногда как
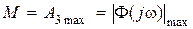 . (7.22)
. (7.22)
Так как 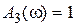 для астатических и
для астатических и 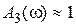 для статических систем при большом коэффициенте усиления K разомкнутой системы, то отличие выражений (7.21), (7.22) друг от друга незначительно.
для статических систем при большом коэффициенте усиления K разомкнутой системы, то отличие выражений (7.21), (7.22) друг от друга незначительно.
Физически показатель колебательности М характеризует склонность системы к колебаниям: чем больше М, тем более колебательный характер переходного процесса. Этот показатель имеет менее прозрачный смысл, чем,
например, время регулирования 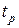 и перерегулирование
и перерегулирование 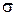 . Считается, что
. Считается, что
если М не превосходит величины 1,2–1,3, то качество процессов в системе будет удовлетворительным и при других внешних воздействиях, отличных от гармонических.
Величина М также косвенно характеризует запасы устойчивости системы: чем больше М, тем меньше запасы устойчивости. Однако количественно связать М и величины 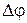 ,
, 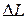 не удается.
не удается.
Для определения величины М можно воспользоваться графиком АЧХ разомкнутой системы 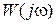 . Пусть
. Пусть 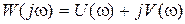 . Тогда
. Тогда 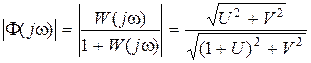 , откуда
, откуда 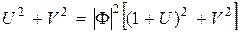 ,
,
или 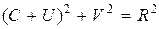 , (7.23)
, (7.23)
где 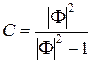 ,
, 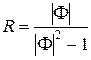 .
.
Задавая 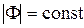 и находя С и R по уравнению (7.23) в комплексной плоскости u, jv, получим кривые, которые будут представлять собой окружности радиусом R с центрами на действительной оси. Эти окружности для разных значений
и находя С и R по уравнению (7.23) в комплексной плоскости u, jv, получим кривые, которые будут представлять собой окружности радиусом R с центрами на действительной оси. Эти окружности для разных значений 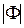 приведены на рис. 7.8.
приведены на рис. 7.8.
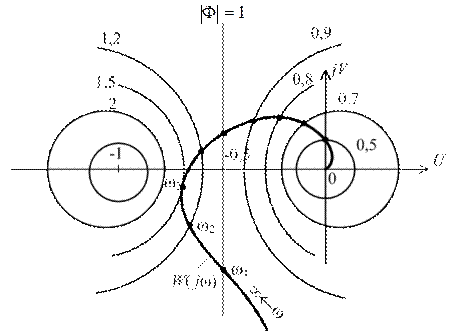
Рис. 7.8
Все эти окружности (линии равных значений 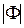 ) охватывают при
) охватывают при 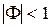 начало координат, а при
начало координат, а при 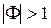 – точку с координатами (–1, j0). При
– точку с координатами (–1, j0). При 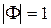 они вырождаются в прямую.
они вырождаются в прямую.
На рис. 7.8 нанесен график АЧХ 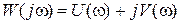 . Фактически представленная серия кривых при
. Фактически представленная серия кривых при 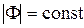 является номограммой для определения
является номограммой для определения 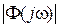 по кривой
по кривой 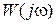 . В точках пересечения
. В точках пересечения 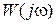 и соответствующей кривой
и соответствующей кривой 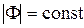 находим для заданного значения
находим для заданного значения 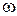 величину
величину 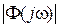 . Так, из рис. 7.8 видим, что при
. Так, из рис. 7.8 видим, что при 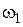 величина
величина 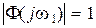 , при
, при 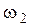 величина
величина 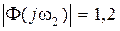 и т.д. Очевидно, что показатель колебательности М определится в точке касания годографа
и т.д. Очевидно, что показатель колебательности М определится в точке касания годографа 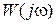 с окружностью, имеющей максимальное значение
с окружностью, имеющей максимальное значение 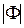 . Для данного случая видно, что это будет окружность, соответствующая M = 1,5.
. Для данного случая видно, что это будет окружность, соответствующая M = 1,5.
Из рис. 7.8 видно, что чем больше величина М (или 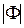 ) для данной системы, тем ближе АФЧХ
) для данной системы, тем ближе АФЧХ 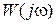 подходит к точке с координатами (–1, j0), тем меньше у системы будут запасы устойчивости.
подходит к точке с координатами (–1, j0), тем меньше у системы будут запасы устойчивости.
Наконец, возможна оценка качественных показателей системы по виду логарифмических частотных характеристик разомкнутой системы. Всю характеристику можно условно разбить по оси частот на три диапазона, как это показано на рис. 7.9, где НЧ – диапазон низких частот, СЧ – средних и ВЧ – высоких частот.
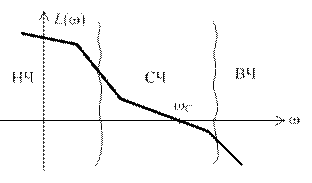 Рис. 7.9
Рис. 7.9
| Логарифмическая характеристика 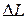 в диапазоне НЧ влияет на точностные характеристики системы, так как первая асимптота определяется двумя величинами: K – коэффициентом усиления разомкнутой системы и в диапазоне НЧ влияет на точностные характеристики системы, так как первая асимптота определяется двумя величинами: K – коэффициентом усиления разомкнутой системы и 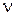 – порядком астатизма. Область средних частот вблизи частоты среза – порядком астатизма. Область средних частот вблизи частоты среза 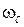 в значительной степени определяет такие показатели системы, как запасы устойчивости в значительной степени определяет такие показатели системы, как запасы устойчивости 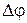 , , 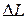 , время регулирования , время регулирования 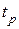 , ,
|
перерегулирование 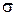 , величину показателя колебательности М. Связать указанные параметры непосредственно с параметрами произвольной ЛАЧХ достаточно трудно. Однако для ряда частных случаев ЛАЧХ путем экспериментальных исследований получены графические зависимости, связывающие указанные величины. Отметим лишь одно общее свойство: чем больше величина
, величину показателя колебательности М. Связать указанные параметры непосредственно с параметрами произвольной ЛАЧХ достаточно трудно. Однако для ряда частных случаев ЛАЧХ путем экспериментальных исследований получены графические зависимости, связывающие указанные величины. Отметим лишь одно общее свойство: чем больше величина 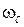 , тем меньше время регулирования. Кроме этого, считается, что для получения приемлемых показателей качества и обеспечения устойчивости желательно, чтобы наклон асимптоты на частоте среза
, тем меньше время регулирования. Кроме этого, считается, что для получения приемлемых показателей качества и обеспечения устойчивости желательно, чтобы наклон асимптоты на частоте среза 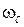 был –20 дБ/дек, а ее протяженность – не менее одной декады.
был –20 дБ/дек, а ее протяженность – не менее одной декады.
Область ВЧ существенного влияния на динамику системы не оказывает, поэтому при анализе ее обычно не учитывают.
Дата добавления: 2015-05-26; просмотров: 1193;
