Критерий устойчивости Найквиста
Критерий устойчивости Найквиста – это частотный критерий, предложенный в 1932 г. Найквистом. Он позволяет судить об устойчивости замкнутой системы управления по виду АФЧХ разомкнутой системы.
Пусть задана передаточная функция разомкнутой системы в виде 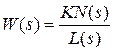 , где L(s) – полином степени n; N(s) – полином степени m,
, где L(s) – полином степени n; N(s) – полином степени m, 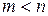 . Тогда ее АФЧХ будет
. Тогда ее АФЧХ будет 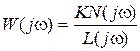 . Составим вспомогательную функцию
. Составим вспомогательную функцию 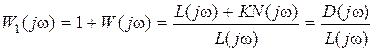 , где D(s) – характеристический полином замкнутой системы, степень которого будет n.
, где D(s) – характеристический полином замкнутой системы, степень которого будет n.
Предположим, что характеристическое уравнение разомкнутой системы 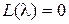 имеет l правых корней и
имеет l правых корней и 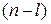 левых корней. Тогда приращение аргумента функции
левых корней. Тогда приращение аргумента функции 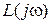 при изменении
при изменении 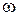 oт
oт 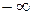 до
до 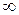 будет
будет 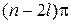 . Если система устойчива в замкнутом состоянии, то характеристическое уравнение замкнутой системы
. Если система устойчива в замкнутом состоянии, то характеристическое уравнение замкнутой системы 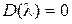 имеет n левых корней и приращение аргумента
имеет n левых корней и приращение аргумента 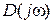 будет paвнo
будет paвнo 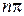 . Найдем приращение аргумента функции
. Найдем приращение аргумента функции 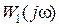 при изменении
при изменении 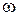 oт
oт 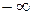 до
до 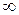 , которое будет в этом случае равно
, которое будет в этом случае равно
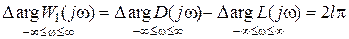 . (5.13)
. (5.13)
В случае, если передаточная функция 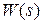 соответствует статической системе (соответствие астатической системе рассмотрим ниже), то при
соответствует статической системе (соответствие астатической системе рассмотрим ниже), то при 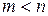 АФЧХ
АФЧХ  при изменении
при изменении 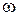 от
от 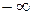 до
до 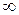 всегда образует замкнутую кривую. Соответственно
всегда образует замкнутую кривую. Соответственно 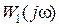 в комплексной плоскости также всегда образует замкнутую кривую. Таким образом, условие (5.13) для замкнутой кривой
в комплексной плоскости также всегда образует замкнутую кривую. Таким образом, условие (5.13) для замкнутой кривой 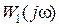 соответствует тому, что вектор
соответствует тому, что вектор 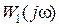 при изменении
при изменении 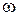 от
от 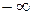 до
до 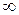 должен в положительном направлении обойти (охватить) начало координат
должен в положительном направлении обойти (охватить) начало координат
l раз. Из связи 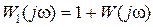 для АФЧХ
для АФЧХ  это соответствует охвату точки с координатами (–1, j0) на комплексной плоскости l раз годографом
это соответствует охвату точки с координатами (–1, j0) на комплексной плоскости l раз годографом  . На основании изложенного сформулируем критерий.
. На основании изложенного сформулируем критерий.
Кpитepий Hайквиста. Если разомкнутая система автоматического управления имеет l правых корней, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы  при изменении частоты
при изменении частоты 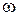 от
от 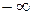 до
до 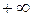 охватывала точку (–1, j0) на комплексной плоскости в положительном направлении l раз.
охватывала точку (–1, j0) на комплексной плоскости в положительном направлении l раз.
Частный случай критерия Найквиста относится к системе, устойчивой в разомкнутом состоянии (l = 0). При этом годограф  не должен охватывать точку (–1, j0).
не должен охватывать точку (–1, j0).
Так как при 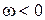 график
график  является зеркальным отображением относительно действительной оси графика при
является зеркальным отображением относительно действительной оси графика при 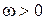 , то обычно достаточно построить
, то обычно достаточно построить  для
для 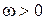 . При этом в формулировке критерия полагают охват точки (–1, j0)
. При этом в формулировке критерия полагают охват точки (–1, j0) 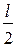 раз.
раз.
На рис. 5.4, а, б представлены графики 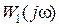 ,
,  в предположении
в предположении
l = 2 для случая устойчивой в замкнутом состоянии системы.
Из изложенного следует, что при корректном применении критерия устойчивости Найквиста следует сначала исследовать устойчивость разомкнутой системы и знать число правых корней ее характеристического уравнения. На практике обычно это нетрудно сделать по виду передаточной функции 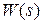 , если она представлена в виде произведения передаточных функций отдельных звеньев.
, если она представлена в виде произведения передаточных функций отдельных звеньев.
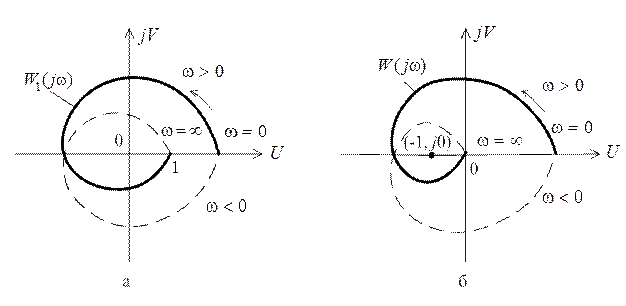
Рис. 5.4
В случае астатической системы формулировка критерия Найквиста сохраняется, однако при этом возникает проблема понятия охвата и неохвата точки (–1, j0), так как при 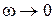 годограф
годограф  уходит в бесконечность и кривая
уходит в бесконечность и кривая  не является замкнутой. В этом случае АФЧХ дополняется дугой бесконечного радиуса по часовой стрелке и после этого проверяется выполнение условия критерия Найквиста. Изображенная на рис. 5.5 система устойчива.
не является замкнутой. В этом случае АФЧХ дополняется дугой бесконечного радиуса по часовой стрелке и после этого проверяется выполнение условия критерия Найквиста. Изображенная на рис. 5.5 система устойчива.
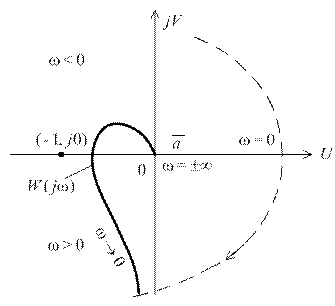 Рис. 5.5
Рис. 5.5
| Для нормального функционирования система управления должна обладать и некоторыми запасами устойчивости, т.е. при изменении параметров системы в процессе работы свойство устойчивости должно сохраняться.
Вполне очевидно, что чем дальше находится кривая  от точки от точки 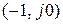 , тем система будет находиться дальше от границы устойчивости. Числовые величины, характеризующие это свойство, носят название запасов устойчивости и могут быть введены различными способами. , тем система будет находиться дальше от границы устойчивости. Числовые величины, характеризующие это свойство, носят название запасов устойчивости и могут быть введены различными способами.
|
На рис. 5.6 представлена АФЧХ разомкнутой системы для устойчивой замкнутой системы.
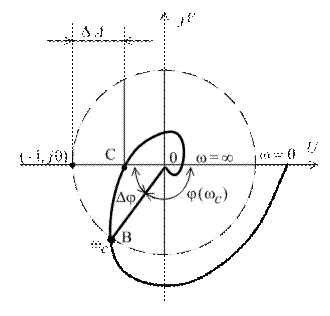 Рис. 5.6
Рис. 5.6
| 3апас устойчивости по фазe определяется как величина угла 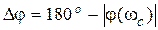 , где , где 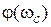 –значение фазы при –значение фазы при 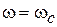 , а частота среза , а частота среза 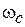 – это значение частоты, при которой – это значение частоты, при которой 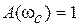 . Из рис. 5.6 видно, что точка В получается пересечением . Из рис. 5.6 видно, что точка В получается пересечением  и окружности единичного радиуса (штриховая линия).
Запас устойчивости по амплитуде и окружности единичного радиуса (штриховая линия).
Запас устойчивости по амплитуде 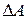 – это величина отрезка оси абсцисс между критической точкой – это величина отрезка оси абсцисс между критической точкой 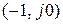 и точкой С пересечения и точкой С пересечения  c осью абсцисс c осью абсцисс
|
(там, где 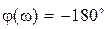 ). Очевидно, в данном случае величина
). Очевидно, в данном случае величина 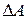 всегда меньше единицы.
всегда меньше единицы.
Если характеристика  имеет более сложные очертания (так называемая клювообразная характеристика представлена на рис. 5.7), то запас по амплитуде характеризуют двумя числами
имеет более сложные очертания (так называемая клювообразная характеристика представлена на рис. 5.7), то запас по амплитуде характеризуют двумя числами 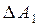 ,
, 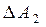 , а запас по фазе
, а запас по фазе 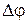 определяется обычным образом.
определяется обычным образом.
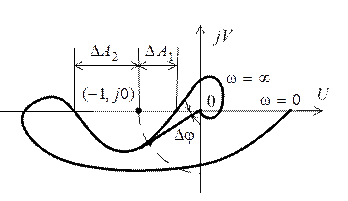 Рис. 5.7
Рис. 5.7
| Рассмотрим интерпретацию критерия Найквиста в логарифмической области. Для простоты рассмотрим систему, устойчивую в paзoмкнутом состоянии, для которой АФЧХ разомкнутой системы  не должна охватывать точку (–1, j0). Очевидно, «опасным» с точки зрения устойчивости является отрезок действительной оси не должна охватывать точку (–1, j0). Очевидно, «опасным» с точки зрения устойчивости является отрезок действительной оси 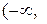 –1), когда фазовая характеристика равна –π, –3π и т.д. При –1), когда фазовая характеристика равна –π, –3π и т.д. При
|
этом модуль 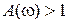 . Пересечение же отрезка действительной оси (–1, 0) годографом
. Пересечение же отрезка действительной оси (–1, 0) годографом  безопасно с точки зрения устойчивости. Если перейти к логарифмическим частотным характеристикам
безопасно с точки зрения устойчивости. Если перейти к логарифмическим частотным характеристикам 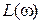 и
и 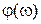 , то характеристики, приведенные на рис. 5.7, будут соответствовать логарифмическим характеристикам, изображенным на рис. 5.8.
, то характеристики, приведенные на рис. 5.7, будут соответствовать логарифмическим характеристикам, изображенным на рис. 5.8.
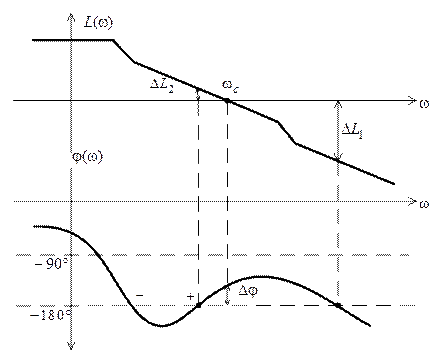
Рис. 5.8
В общем случае критерий Найквиста применительно к логарифмическим характеристикам формулируется так: для устойчивости замкнутой системы необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов логарифмической фазовой частотной характеристикой 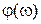 разомкнутой системы прямых
разомкнутой системы прямых 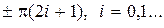 во всех областях,
во всех областях, 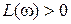 была равна
была равна 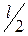 (l – число правых корней характеристического уравнения разомкнутой системы).
(l – число правых корней характеристического уравнения разомкнутой системы).
Отметим, что 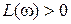 обычно до частоты среза системы
обычно до частоты среза системы 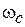 . Если система устойчива в разомкнутом состоянии, то l = 0.
. Если система устойчива в разомкнутом состоянии, то l = 0.
При использовании логарифмических характеристик также вводят запасы устойчивости, показанные на рис. 5.8. При 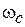 запас устойчивости по фазе определяется как
запас устойчивости по фазе определяется как 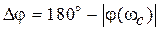 , а запас устойчивости по модулю характеризуется величинами отрезков
, а запас устойчивости по модулю характеризуется величинами отрезков 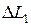 ,
, 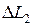 , выраженными в децибелах. В случае обычных, не клювообразных, характеристик
, выраженными в децибелах. В случае обычных, не клювообразных, характеристик  запас устойчивости по модулю характеризуется одной величиной
запас устойчивости по модулю характеризуется одной величиной 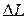 , определяемой на критической частоте
, определяемой на критической частоте 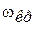 , соответствующей
, соответствующей 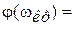 –180o.
–180o.
На практике величина запасов устойчивости по фазе и модулю обычно колеблется в пределах 30o…60o и (6…20) дБ. Величина (6...20) дБ соответствует усилению в (2...10) раз.
Рассмотрим, как в общих чертах влияют параметры и вид АФЧХ разомкнутой системы  на устойчивость. Если
на устойчивость. Если 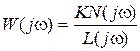 , то очевидно, что величина коэффициента усиления не влияет на вид фазовой частотной характеристики. Модуль
, то очевидно, что величина коэффициента усиления не влияет на вид фазовой частотной характеристики. Модуль  пропорционален величине K. Таким образом, увеличение (уменьшение) величины K будет пропорционально увеличивать (уменьшать)
пропорционален величине K. Таким образом, увеличение (уменьшение) величины K будет пропорционально увеличивать (уменьшать) 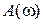 , не изменяя фазового угла годографа вектора
, не изменяя фазового угла годографа вектора  в комплексной плоскости. кривая
в комплексной плоскости. кривая  (см. рис. 5.6) будет пропорционально расширяться или сжиматься, и с увеличением K наступит момент, когда
(см. рис. 5.6) будет пропорционально расширяться или сжиматься, и с увеличением K наступит момент, когда  охватит точку (–1, j0) и система станет неустойчивой. Это следует и по ЛАЧХ (см. рис. 5.8). Увеличение K поднимает характеристику
охватит точку (–1, j0) и система станет неустойчивой. Это следует и по ЛАЧХ (см. рис. 5.8). Увеличение K поднимает характеристику 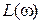 , приводит к смещению
, приводит к смещению 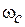 вправо по оси абсцисс и в конечном счете к потере устойчивости.
вправо по оси абсцисс и в конечном счете к потере устойчивости.
В случае клювообразных характеристик (см. рис. 5.7, 5.8) возможна потеря устойчивости и при уменьшении общего коэффициента усиления. Увеличение порядка астатизма системы также отрицательно сказывается на устойчивости, так как приводит к увеличению отрицательных фазовых сдвигов.
Дата добавления: 2015-05-26; просмотров: 1459;
