Критерий устойчивости Михайлова
Этот критерий относится к группе частотных и был предложен в 1938 г. А. Михайловым. Он базируется на известном в теории функции комплексного переменного принципе аргумента. Характеристический полином замкнутой системы представим в виде 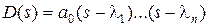 , где
, где 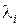 – корни уравнения
– корни уравнения 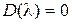 .
.
Сделаем замену 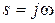 , тогда
, тогда 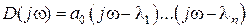 . Приращение аргумента вектора
. Приращение аргумента вектора 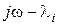 при изменении частоты
при изменении частоты 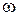 от
от 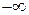 до
до 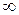 будет равно
будет равно 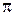 для левого корня и
для левого корня и 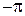 для правого корня (рис. 5.1). Приращение аргумента вектора
для правого корня (рис. 5.1). Приращение аргумента вектора 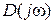 , имеющего
, имеющего 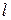 правых и
правых и 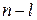 левых корней, будет равно
левых корней, будет равно 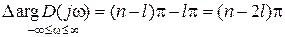 , а при изменении
, а при изменении 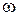 от 0 до
от 0 до 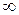 – в 2 раза меньше, т.е.
– в 2 раза меньше, т.е. 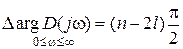 .
.
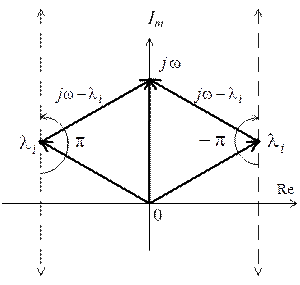 Рис. 5.1
Рис. 5.1
| Из последнего выражения следует, что для устойчивой САУ 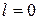 и и
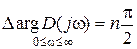 . (5.12)
Полином D(s) после замены . (5.12)
Полином D(s) после замены  представляет собой комплексное число, действительная и мнимая части которого зависят от частоты представляет собой комплексное число, действительная и мнимая части которого зависят от частоты 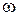 : :
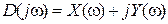 ,
где ,
где 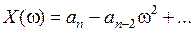 , ,
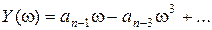 . .
|
Изменяя 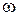 от нуля до
от нуля до 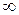 , на комплексной плоскости строится годограф, который называется кpивой Mиxайлова. При
, на комплексной плоскости строится годограф, который называется кpивой Mиxайлова. При 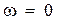 он всегда будет находиться на действительной оси в точке
он всегда будет находиться на действительной оси в точке  , а при
, а при 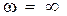 значения Х и Y равны
значения Х и Y равны 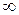 или
или 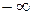 , т.е. годограф будет уходить в бесконечность в каком-либо квадранте комплексной плоскости.
, т.е. годограф будет уходить в бесконечность в каком-либо квадранте комплексной плоскости.
Кpитepий Миxайлова. Для устойчивости линейной системы необходимо
и достаточно, чтобы приращение аргумента функции 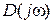 при изменении
при изменении
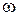 от нуля до
от нуля до 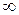 равнялось
равнялось 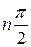 , что означает последовательное прохождение кривой Михайлова n квадрантов против часовой стрелки в комплексной
, что означает последовательное прохождение кривой Михайлова n квадрантов против часовой стрелки в комплексной
плоскости.
Обычно критерий Михайлова применяется после проверки необходимого условия устойчивости (5.3).
На рис. 5.2 представлен ряд кривых Михайлова для систем различного порядка.
Кривые 1, 2 соответствуют устойчивым системам при n = 3, 4 соответственно, кривая 3 – неустойчивой системе при 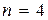 , так как нарушена последовательность прохождения квадратов комплексной плоскости.
, так как нарушена последовательность прохождения квадратов комплексной плоскости.
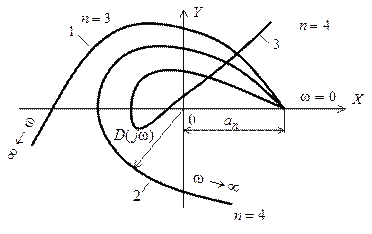 Рис. 5.2
Рис. 5.2
| Рассмотрим определение с помощью кривой Михайлова границ устойчивости. Система будет находиться на границе устойчивости, если чисто мнимая величина 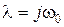 будет являться корнем уравнения будет являться корнем уравнения 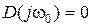 , т.е. кривая Михайлова должна проходить через начало координат. При этом при , т.е. кривая Михайлова должна проходить через начало координат. При этом при 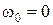 имеем апе- имеем апе-
|
риодическую границу, при 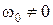 – колебательную,
– колебательную, 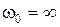 соответствует бесконечному корню. При этом следует проверить, чтобы все остальные корни были левыми. Такую проверку можно осуществить, исследуя соответствующий график кривой Михайлова в точке пересечения начала координат. Если малые деформации кривой приводят к устойчивой системе, то это соответствует границе устойчивости.
соответствует бесконечному корню. При этом следует проверить, чтобы все остальные корни были левыми. Такую проверку можно осуществить, исследуя соответствующий график кривой Михайлова в точке пересечения начала координат. Если малые деформации кривой приводят к устойчивой системе, то это соответствует границе устойчивости.
На рис. 5.3 представлены два годографа, проходящие через начало координат.
 Рис. 5.3
Рис. 5.3
| Для кривой 1 малые деформации ее в начале координат приведут к устойчивой системе, что соответствует границе устойчивости, а для кривой 2 система при малых деформациях графика все равно будет неустойчивой.
Пример 5.4. Передаточная функция разомкнутой системы имеет вид  . Характеристический полином замкнутой системы будет . Характеристический полином замкнутой системы будет  и соответственно и соответственно  . При любом . При любом
|
 ,
, 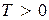 кривая Михайлова при
кривая Михайлова при 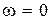 будет начинаться на действительной оси в точке с координатами (K, j0) и всегда проходить последовательно первый и второй квадранты комплексной области, так как мнимая часть
будет начинаться на действительной оси в точке с координатами (K, j0) и всегда проходить последовательно первый и второй квадранты комплексной области, так как мнимая часть 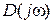 всегда положительна, а действительная с ростом W меняет знак с плюса на минус.
всегда положительна, а действительная с ростом W меняет знак с плюса на минус.
Система при любых K > 0, T > 0 всегда устойчива, что совпадает с результатом примера 5.1.
Дата добавления: 2015-05-26; просмотров: 1267;
