Моделирование переходных процессов на ПЭВМ
С помощью известной системы математических расчетов Matlab, в которую встроен специальный пакет для исследования систем автоматического управления – Control System Toolbox, можно по передаточной функции системы построить необходимые графики временных характеристик. В Matlab также можно представить эквивалентную модель системы в среде Simulink и исследовать ее характеристики в этом приложении.
Рассмотрим применение описанных возможностей работы в Matlab на примере системы, структурная схема которой задана в виде последовательного соединения двух апериодических звеньев с параметрами: K1 = 2; K2 = 50; 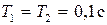 (рис. 4.3).
(рис. 4.3).
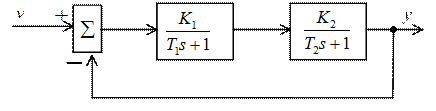
Рис. 4.3
Для этой системы построим график переходной функции 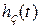 двумя способами.
двумя способами.
1. При использовании операторов пакета Control System Toolbox запишем в командном окне следующую программу:
K1 = 2; K2 = 50; T1 = 0,1; T2 = 0,1;
w= tf([K1*K2], [T1*T2 (T1+T2) 1]);
w1= feedback(w,1);
step(w1)
В первой строке происходитопределение параметров системы и присвоение им численных значений.
Если передаточную функцию разомкнутой системы представить в виде отношения полиномов по степеням s :
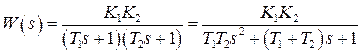 ,
,
то удобно использовать оператор tf, который позволяет записывать передаточные функции путем формирования векторов коэффициентов числителя и знаменателя так, как это представлено во второй строке программы.
В третьей строке оператор feedback замыкает систему с единичным коэффициентом усиления в цепи обратной связи.
Оператор step позволяет построить переходной процесс системы при подаче на ее вход единичной ступенчатой функции 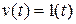 .
.
График переходного процесса, полученный в результате выполнения программы, представлен на рис. 4.4.
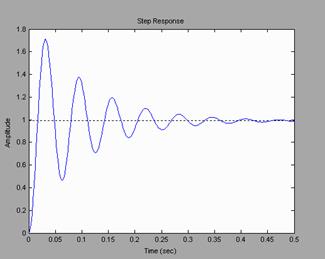
Рис. 4.4
2. Представим модель системы в среде Simulink, как показано на рис. 4.5, используя стандартные блоки из библиотеки ее приложения.
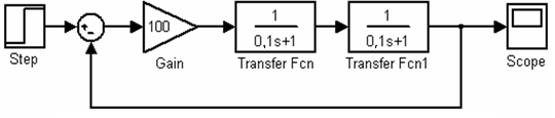
Рис. 4.5
При моделировании получим на экране виртуального осциллографа (Scope) график переходного процесса (рис. 4.6), который совпадает с приведенным на рис. 4.4.
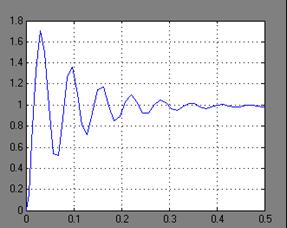
Рис. 4.6
Аналогичным образом могут быть построены и другие характеристики системы. Более подробно основы работы в системе Matlab рассматриваются в
[8].
Дата добавления: 2015-05-26; просмотров: 1161;
