Общее описание процессов
Динамические процессы в стандартной системе автоматического управления, структурная схема которой приведена на рис. 3.1, описываются во временной области дифференциальным уравнением
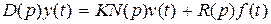 (4.1)
(4.1)
или в области изображений выражением
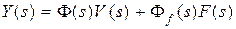 . (4.2)
. (4.2)
Выходной сигнал y(t) замкнутой системы, являющийся решением линейного дифференциального уравнения (4.1),может возникнуть в системе либо за счет внешних воздействий v(t) или f(t), либо за счет вариации начальных условий переменной y(t) и ее производных. Составляющую выходного сигнала, обусловленную ненулевыми начальными условиями переменной y(t) и ее производных, будем называть свободной и обозначать yС(t), а составляющие, обусловленные сигналами v(t) и f(t), – вынужденными и обозначать соответственно yvв(t) и yfв(t). Тогда процесс y(t), являющийся решением линейного дифференциального уравнения (4.1),определяется выражением
y(t) = yС (t) + yв(t) = yС (t) + yvв(t) + yfв(t), (4.3)
где yв(t) = yvв(t) + yfв(t).
В математике yС (t) называют общим решением уравнения (4.1)без правой части (однородного уравнения), a yв(t) – частным решением уравнения (4.1) с правой частью (неоднородного уравнения).
Общее решение однородного уравнения в случае простых (различных) корней характеристического уравнения 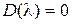 , которые обозначим через
, которые обозначим через 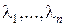 , определяется выражением
, определяется выражением
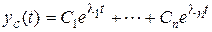 , (4.4)
, (4.4)
где Сi – произвольные постоянные, определяемые через начальные условия 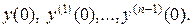
Если характеристическое уравнение 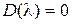 имеет один кратныйкорень, например
имеет один кратныйкорень, например 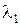 кратности r, а остальные
кратности r, а остальные 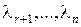 – простые, то общее решение будет иметь вид
– простые, то общее решение будет иметь вид
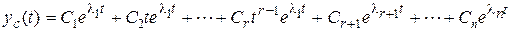 . (4.5)
. (4.5)
В случае нескольких кратных корней в свободной составляющей будут появляться аналогичные группы слагаемых, соответствующие каждому кратному корню.
Длявычисления вынужденной составляющей обратимся к уравнению
относительно изображений (4.2). Обозначим весовые функции замкнутой системы по управляющему сигналу 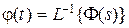 и по возмущению
и по возмущению 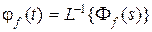 , тогда переходя в (4.2)к оригиналам, с учетом того, что произведение изображений есть свертка во временной области, получим
, тогда переходя в (4.2)к оригиналам, с учетом того, что произведение изображений есть свертка во временной области, получим
yв(t) = yvв(t) + yfв(t) 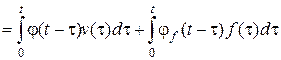 . (4.6)
. (4.6)
Таким образом, полное решение 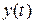 дифференциального уравнения будет иметь вид
дифференциального уравнения будет иметь вид
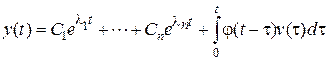
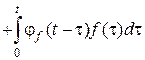 . (4.7)
. (4.7)
В случае нулевых начальных условий ( 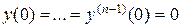 ) все
) все 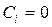 и (4.7) превращается в соотношение (4.6).
и (4.7) превращается в соотношение (4.6).
При исследовании систем управления обычно ограничиваются внешними воздействиями определенного типа, что дает возможность ввести некоторые показатели качества процессов управления и оказывается удобным для сравнительного анализа проектируемых систем. Наиболее часто сигнал уп  равления v(t) (то же самое и для возмущения
равления v(t) (то же самое и для возмущения 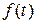 ) задают в виде типового сигнала следующего вида:
) задают в виде типового сигнала следующего вида:
v(t) = 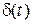 – дельта-функция;
– дельта-функция;
v(t) = v01[t]– ступенчатая функция амплитуды v0 (скачок по положению);
v(t) = v1t – скачок по скорости;
v(t) = v2t2 – скачок по ускорению;
v(t) = v0+v1t + v2t2 +…+ vktk – полиномиальное воздействие;
v(t) 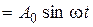 – гармоническое воздействие, где А0 амплитуда,
– гармоническое воздействие, где А0 амплитуда, 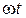 – фаза,
– фаза, 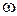 – частота;
– частота;
v(t) 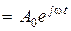 – гармоническое воздействие в комплексной форме.
– гармоническое воздействие в комплексной форме.
Вэтих выражениях сигналы определены при t > 0 и paвны нулю при 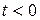 , a vi = const, A0 = const,
, a vi = const, A0 = const, 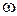 = const.
= const.
Выбор того или иного сигнала зависит от вида системы и условий ее функционирования. Например, для систем стабилизации наиболее естественной формой управляющего воздействия является ступенчатая функция. Для следящих систем таковыми являются сигналы гармонического типа.
Наиболее часто динамические свойства системы оцениваются по ее реакции на единичную ступенчатую функцию v(t) =1[t], т.е. по виду выходного сигнала 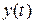 , являющегося переходной функцией замкнутой системы hз (t).
, являющегося переходной функцией замкнутой системы hз (t).
На рис. 4.1 представлен наиболее типичный вид переходной функции hз (t), где 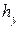 – установившееся значение выходной координаты.
– установившееся значение выходной координаты.
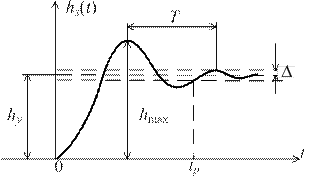 Рис. 4.1
Рис. 4.1
| Для оценки качества регулирования по виду hз(t) вводят показатели качества:
tр – время регулирования (время переходного процесса), это время, после которого величина 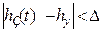 , где обычно ∆ = 5 % от hy; , где обычно ∆ = 5 % от hy;
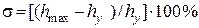 – перерегулирование в процентах; – перерегулирование в процентах;
|
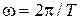 – частота колебаний переходного процесса;
– частота колебаний переходного процесса;
число колебаний за время переходного процесса.
Наиболее важными показателями качества являются tр и 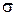 . Величина tр может изменяться в широких пределах в зависимости от вида системы управления. Перерегулирование обычно лежит в пределах от 0 до 30 %. Число колебаний за время регулирования обычно 1–2, а иногда 3–4. В некоторых случаях колебания недопустимы.
. Величина tр может изменяться в широких пределах в зависимости от вида системы управления. Перерегулирование обычно лежит в пределах от 0 до 30 %. Число колебаний за время регулирования обычно 1–2, а иногда 3–4. В некоторых случаях колебания недопустимы.
По виду функции hз(t) процессы делятся на три категории (рис. 4.2):
монотонные (1), апериодические (2)и колебательные (3).
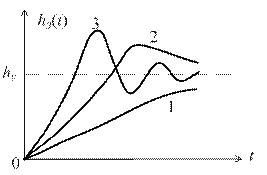 Рис. 4.2 Рис. 4.2
| У монотонных процессов 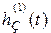 не меняет знак, у апериодического процесса знак производной не меняет знак, у апериодического процесса знак производной 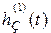 изменяется только один раз, у колебательного – бесконечное число раз.
Вычисление процессов в замкнутой системе фактически представляет собой задачу решения дифференциального уравнения (4.1) при заданных входных воздействиях v(t) и f(t) и начальных усло- изменяется только один раз, у колебательного – бесконечное число раз.
Вычисление процессов в замкнутой системе фактически представляет собой задачу решения дифференциального уравнения (4.1) при заданных входных воздействиях v(t) и f(t) и начальных усло-
|
виях. Существующие методы решения этой задачи можно разбить на две категории: аналитические методы и методы моделирования на ПЭВМ.
Пример 4.1. В системе (см. рис. 3.1)будем полагать 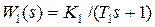 ;
; 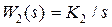 ; Т1 = 0,01 c; K1 = 10; K2 = 0,475, где K1 и K2 имеют соответствующую размерность.
; Т1 = 0,01 c; K1 = 10; K2 = 0,475, где K1 и K2 имеют соответствующую размерность.
Найдем выражение, связывающее выходной сигнал 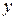 с внешними
с внешними
воздействиями v и f. для определения свободной составляющей (произвольных Сi) воспользуемся операционным методом решения дифференциального уравнения.
Выражение (4.2) будет иметь вид
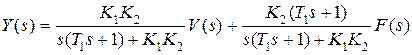 ,
,
из которого дифференциальное уравнение замкнутой системы (4.1) будет 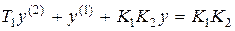 v
v 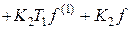 .
.
Будем полагать начальные условия для выходного сигнала 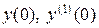 ненулевыми, а для входного сигнала – нулевыми. применим к дифференциаль-
ненулевыми, а для входного сигнала – нулевыми. применим к дифференциаль-
ному уравнению преобразование Лапласа.
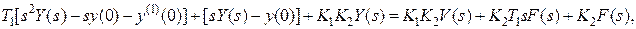
откуда
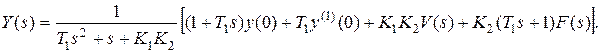
Полученное выражение отличается от первоначального в этом примере наличием членов, учитывающих ненулевые начальные условия. С учетом заданных параметров T1, K1, K2 будем иметь
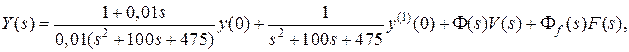
где 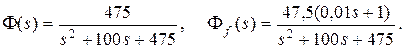
Применяя обратное преобразование Лапласа, получим в области
оригиналов
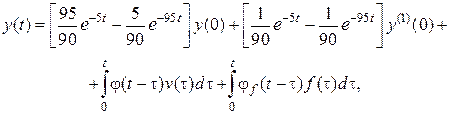
где 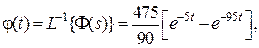
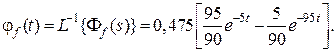
Дата добавления: 2015-05-26; просмотров: 970;
