Оценка надежности технических систем при мгновенном восстановлении устройств

Решения задач определения надежности технических систем, рассмотренные в предыдущих разделах, были построены на том, что отказавшие устройства выходили из строя окончательно, без рассмотрения возможности их восстановления или ремонта. Таким образом, все процессы, связанные с надежностью систем, которые исследовались до сих пор, были существенно нестационарными, поскольку при отсутствии восстановления в случае t ® ¥ надежность системы стремилась к нулю, и «предельным режимом» работы системы был отказ, т.е. система не работала.

В задачах с восстановлением нас будут интересовать не только переходные процессы в технической системе, но и ее работа в установившемся режиме при t ® ¥ .

Рассмотрим задачу, представляющую некоторый переход от задач оценки надежности резервированных систем к задачам определения надежности технических систем с восстановлением.

Пусть работает простая система, состоящая из одного основного устройства, которое подвергается простейшему потоку отказов с интенсивностью l. При отказе это устройство мгновенно заменяется новым с такими же характеристиками. Пусть имеется m запасных устройств (система состоит из одного основного и m резервных устройств, т.е. всего m+1 устройство).

Требуется определить вероятность того, что этого числа m запасных устройств будет достаточно для обеспечения работы системы в течение времени t, т.е. требуется определить надежность P(t) системы с восстановлением.

Нетрудно заметить, что поставленная задача адекватна задаче оценки надежности резервированной технической системы с m резервными устройствами, работающими в режиме «холодного» резерва с идеальными коммутаторами. Однако, для решения этой задачи воспользуемся несколько иным и более простым методом.

Рассмотрим на оси “0-t” «поток восстановлений», или последовательность моментов времени, в которые выходят из строя и мгновенно восстанавливаются устройства системы (рис. 10.1). Очевидно, рассматриваемый поток относится к простейшим с интенсивностью l.

Рис. 10.1. Представление потока восстановления простейшей системы

Надежность P(t) технической системы есть вероятность того, что к моменту t система будет находиться в рабочем состоянии. Для этого необходимо, чтобы на участке (0, t) отказало не более m устройств из общего числа (m+1), т.е. должно остаться в работе хоть одно устройство.

Как известно, число событий n простейшего потока, попадающих на участок продолжительностью t, распределено по закону Пуассона. При этом вероятность попадания ровно n событий на рассматриваемый временной интервал определяется зависимостью:

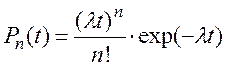(10.1)
где n = 0, 1, 2,…, m,….

Найдем вероятность того, что число точек (событий замены отказавших устройств), попадающих на участок (0, t), будет не больше числа m+1, т.е. всего может отказать m устройств. Эта вероятность и будет надежностью рассматриваемой технической системы:

(10.2)
или короче:

(10.3)
где P_n(t) раскрыта с помощью (10.1).

В выражении (10.2) правая часть определяет, что произойдет или ни одного события (P₀), или одно событие (P₁), или два события (P₂) и т.д. или m событий замены отказавших устройств (Р_m), что соответствует нахождению в рабочем состоянии хотя бы одного устройства, что и есть «не более m+1» отказа.

Подставив в (10.3) выражение (10.1), получим:

(10.4)
Пример 10.1.

Рассматривается работа технической системы с восстановлением (рассмотренная выше задача). Интенсивность потока отказов l = 2 , 1/год (два отказа в год). Имеется 5 запасных устройств (всего устройств в системе m+1 = 6). Максимальное время работы системы t = 5 лет.

Определить функцию надежности системы P(t).

Решение.

Разобьем рассматриваемый временной интервал на равные промежутки времени с шагом 1 год и вычислим по формуле (10.4) соответствующие значения надежности системы.

Результаты расчетов представлены в табл.10.1 и на рис.10.2.

Таблица 10.1

Результаты решения примера 10.1

Рассмотрим еще одну задачу.

Пусть техническая система состоит из нескольких устройств, среди которых: m₁+1 устройств типа 1, m₂+1устройств типа 2,..., m_k+1 устройств типа k.

Устройство каждого типа, независимо от других, может выходить из строя с соответствующими интенсивностями l₁, l₂,…,l_k. Все потоки отказов устройств –– простейшие. Отказавшее устройство немедленно заменяется новым. В резерве к системе имеется m₁, m₂,…,m_k запасных устройств соответствующего типа. При этом отсутствие запасного устройства при очередном отказе означает отказ системы.

Требуется определить надежность технической системы на интервале времени (0, t).

Решение этой задачи строится на представлении системы в виде последовательно соединенных элементов, каждый из которых представляет собой устройство конкретного типа. Тогда надежность системы будет равна произведению надежностей всех групп (всех типов) устройств.

Рис.10.2. Вид функции надежности технической системы с восстановлением, состоящей из одного основного и пяти запасных устройств

Надежность i-й группы определяется согласно (10.4):

(10.5)
Перемножая эти вероятности, получим формулу для расчета надежности технической системы:

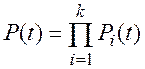(10.6)
Заметим, что, пользуясь приведенными выше формулами, можно не только оценивать надежность системы при заданном числе m запасных устройств, но и определить, сколько запасных устройств необходимо иметь для того, чтобы обеспечить заданное значение надежности на требуемом временном интервале.