Значимость элемента в системе.

В 1969 г. проф. Бирнбаум определил надежностную значимость 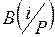элемента x_i в системе с монотонной структурой как частную производную:

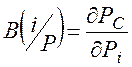(9.12)
где Р_C –– вероятность безотказной работы системы, зависящая, в частности, от надежности i-го элемента Р_i.

В том случае, когда значения P_i равнозначны, вычисляется так называемая структурная значимость B(i) i-го элемента:

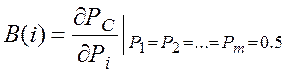(9.13)
т.е.

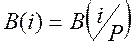(9.14)
с вероятностями безотказной работы всех элементов, равными 0.5.

Рациональность использования логико-вероятностных методов можно продемонстрировать на следующем простом примере.

Дана сложная структурная система (участок магистрального трубопровода), состоящая из пяти элементов х1, х2,..., х5, представленная схематично на рис. 9.1.

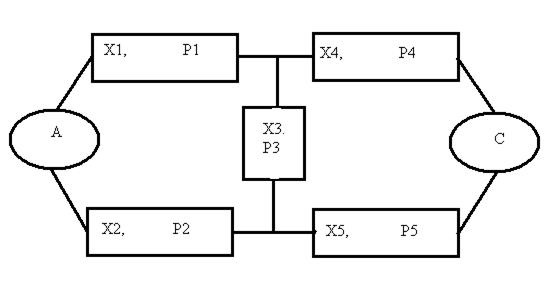
Рис. 9.1. Блок-схема развязки лупингов трубопроводной системы

Требуется определить надежность Р_С участка магистрального трубопровода от узла А до узла С, если известны вероятности безотказной работы (надежность) отдельных участков (Р1=0.8, Р2=0.85, Р3=0.9, Р4=0.75, Р5=0.7).

Решение.

Минимальные пути, сохраняющие работоспособность системы:

х1Ùх4, х2Ùх5, х1Ùх3Ùх5, х2Ùх3Ùх4 (9.15)
Следовательно, трубопроводная система сохраняет работоспособность при выполнении следующей логики:

(х1Ùх4)Ú(х2Ùх5)Ú(х1Ùх3Ùх5)Ú(х2Ùх3Ùх4) (9.16)
Надежность системы, с учетом исходных значений вероятностей безотказной работы отдельных участков принимает вид:

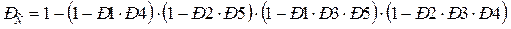(9.17)

Р_С = 0.96575.

При отсутствии элемента х3 итоговая надежность участка была бы равна:

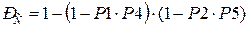=0.838 (9.18)
Определим значимость элементов, например, х1 и х3.

Надежностная значимость элемента х1:

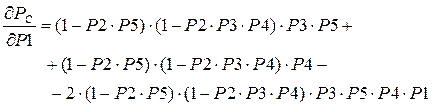(9.19)
Надежностная значимость элемента х₃:

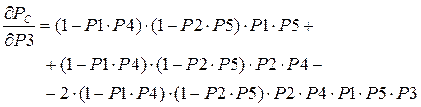(9.20)
После подстановки исходных данных по значениям надежности отдельных элементов, получим:

- надежностная значимость элемента х1 = 0.1077;

- надежностная значимость элемента х3 = 0.0898.

Для определения структурной значимости элементов подставим в полученные выражения значения вероятностей всех элементов, равные 0.5, получим структурную значимость элемента х1, равную 0.41016; структурную значимость элемента х3, равную 0.2461.

На основании проведенных расчетов можно сделать вывод о том, что в надежности системы элемент х3 в сравнении с элементом х1 играет при данных значениях надежности остальных элементов не столь существенную роль, а в структурной значимости элементов системы роль элемента х3 существенно менее значима в сравнении с элементом х1.

Аналогичные расчеты по оценке значимости можно произвести для всех элементов рассматриваемой системы.