Некоторые сведения из основ алгебры логики.

Алгебра логики –– это раздел математической логики, изучающий логические операции над высказываниями. Ее основоположником является Джордж Буль, впервые применивший алгебраические методы для решения традиционных логических задач.

Логические операции позволяют из нескольких высказываний образовывать новые высказывания. В алгебре логики, где интересуются только истинностным значением высказываний, исследуется вопрос об истинностном значении сложного высказывания в зависимости от истинности значений составляющих его простых высказываний.

В алгебре логики принято истину обозначать числом 1, а ложь –– числом 0.

Каждой логической операции соответствует функция, принимающая значения 0 или 1, аргументы которой также принимают значения только 0 или 1. Такие функции называются логическими функциями (или булевыми функциями, или функциями алгебры логики).

Алгебра логики строится на нескольких простых операциях:

- конъюнкция (логическое умножение), обозначается знаком Ù;

- дизъюнкция (логическое сложение), обозначается знаком Ú;

- отрицание, обозначается знаком - ;

- эквивалентность, обозначается знаком ~;

- импликация, обозначается знаком ®.

Перечисленные операции могут быть представлены таблицей

Таблица 9.1

Истинностная таблица функций алгебры логики.

x	y	x Ù y	x Ú y		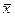x ~ y	x ® y

С помощью уравнений алгебры логики можно описать условия работоспособности или опасности системы. Уравнения ФАЛ показывают, из каких элементов (инициирующих условий) и какими соединениями можно обеспечить выполнение заданного технической системе назначения, а также оценить причины перехода системы в опасное состояние.