Метод РМА тонких плівок і малих частинок

Кількісний РМА масивних матеріалів обмежений дослідженням зразків із плоскою поверхнею, розміщеною під відомим кутом стосовно до первинного пучка електронів і рентгенівського спектрометра. За таких умов величини І_і та І_0і різняться між собою тільки у зв’язку з різним хімічним складом.

Поряд із цим існує широкий клас зразків неправильної форми, які не задовольняють наведені геометричні вимоги. До цього класу відносять малі частинки (МЧ), шорсткі поверхні, поверхні зломів масивних зразків і, за деяких умов, тонкі плівки у вільному стані (їх у методиці РМА прийнято називати фольгами) або на підкладці, порошкові або пористі матеріали.

Розглянемо особливості РМА фольг і тонких плівок на підкладці (плівка/П, де П - підкладка). Методи аналізу в цих випадках значно відрізняються. Зразок вважається тонкою плівкою або фольгою, якщо його товщина менша від поздовжнього розміру області взаємодії електронів у масивному зразку такого самого хімічного складу.

РМА тонких фольг являє собою просту аналітичну задачу. Це пов’язано з тим, що у тонких зразках пружне розсіювання і втрати енергії зменшуються до такої міри, що можна знехтувати впливом усіх трьох поправок, а РМА провести методом відносної чутливості Г. Кліффа і Г. Лорімера, використовуючи фактор відносної елементної чутливості елемента і до елемента j

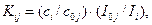(7.7)

де с_і та с_0j – вагова концентрація і-го елемента та відома концентрація j-го елемента, який використовується як еталон (як правило - Si); І_і та І_0j – скориговані на фон інтенсивності рентгенівського випромінювання, К_ij – фактор відносної елементної чутливості, який вимірюється на еталонах у вигляді тонких фольг відомого хімічного складу.

Із рівняння (7.7) отримуємо співвідношення с_і

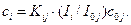(7.7′)

При наявності у зразку n елементів, концентрація одного із яких (х) невідома, рівняння (7.7′) нормується на одиницю, що дає можливість розрахувати с_х. Відмічаємо, що співвідношення (7.7′) спрацьовує до певної критичної товщини фольги, починаючи з якої необхідно вводити поправку на поглинання первинних електронів і на флуоресценцію.

У випадку плівки на підкладці мають місце складніші процеси взаємодії первинних електронів (рис. 7.4), що значно ускладнює проведення РМА. Тут можливі варіанти,

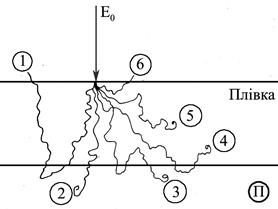
Рисунок 7.4 – Можливі траєкторії електронів у тонкій плівці на підкладці: 1, 6 – відбиті електрони; 2–5 – електрони, які залишаються в плівці або підкладці

коли електрони збуджують рентгенівське випромінювання в плівці одразу або після відбиття від підкладки; після розсіювання в плівці або, пройшовши плівку, розсіюються від підкладки; можуть неоднократно пересікати межу поділу плівка/П, перед тим як втратити енергію. Частота кожного із зазначених процесів залежить від товщини і хімічного складу плівки та підкладки. У зв’язку із складністю проблеми найбільш ефективним методом аналізу залишається моделювання можливих траєкторій електронів методом Монте-Карло. Ряд авторів отримали аналітичний вираз для відношення І_і/І_0і, який багатопараметричний і має надзвичайно складний вигляд, а тому його недоцільно наводити у даному посібнику, оскільки систематичне викладання обох методів не наводиться навіть у цитованих нами фундаментальних монографіях, його можна знайти лише в оригінальних статтях.

У ряді випадків, коли аналізується одношарова плівка на підкладці із масовою товщиною до 30% об’єму взаємодії електронів у масивному зразку, можна користуватися емпіричним методом Г. Яковіца і Д. Ньюбері, в основу якого покладено порівняння кривих експериментального і розрахункового розподілів інтенсивності рентгенівського випромінювання за глибиною зразка.

При РМА малих частинок немає можливості розрізати їх, відполірувати й отримати плоску поверхню, як у випадку масивних зразків. Це є головною причиною виникнення т.зв. геометричних ефектів при аналізі малих частинок, які поділяють на дві групи: масовий ефект та ефект поглинання.

Масовий ефект виникає тоді, коли розміри МЧ наближаються до розмірів області взаємодії у твердому тілі й електрони можуть виходити за межі частинок (рис. 7.5), що призведе до зменшення величини І_і порівняно із масивними зразками (рис. 7.6 ілюструє цей ефект на прикладі атомів Fe у МЧ скла різного діаметра). Масовий ефект завжди призводить до зниження І_і і стає значним при D < 5 мкм, якщо Е₀ ≤ 20 кеВ.

Ефект поглинання виникає в результаті того, що довжина пробігу рентгенівського фотона в МЧ, на якому відбувається його поглинання, буде відрізнятися порівняно із масивними зразками. Але оскільки поглинання

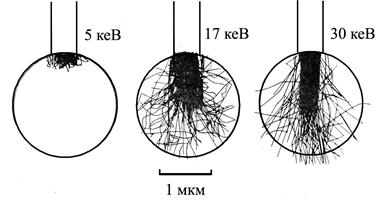
Рисунок 7.5 – Електронні траєкторії в області взаємодії електронів у МЧ Al, розраховані Д. Ньюбері та С. Ґрінвольдом методом Монте-Карло

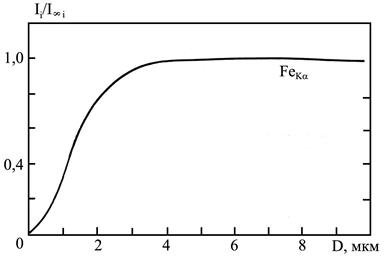
Рисунок 7.6 – Залежність відносної інтенсивності рентгенівського випромінювання атомів Fe від діаметра (маси) МЧ скла. І_∞і – інтенсивність випромінювання масивного зразка

експоненціально залежить від довжини пробігу, то геометрія МЧ може сильно впливати на величину рентгенівського випромінювання. Тут мають місце два різновиди ефекту поглинання: ефект положення пучка електронів та ефект розміру МЧ. Перший із них пов'язаний із місцеположенням точки потрапляння первинного пучка електронів відносно детектора. Рисунок 7.7 ілюструє цей ефект. Для зменшення впливу ефекту положення пучка РМА проводиться растром при швидкому скануванні, в результаті чого збуджується спектр при всіх положення зонда. Рисунок 7.8 ілюструє залежність І_і/І_0і для атомів Si в Fe, коли фіксується точка потрапляння первинного пучка, але змінюється кут входу (ψ) рентгенівських променів.

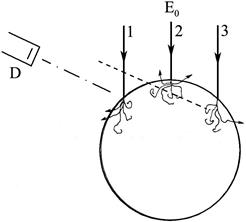
Рисунок 7.7 – Різниця в шляху поглинання рентгенівського випромінювання при потраплянні первинного пучка на передній відносно детектора (Д) бік (1), на вершину (2) або на протилежний детектору бік (3) МЧ

Другий ефект поглинання – ефект розміру частинок – проявляється залежністю І_і/І_∞і від діаметра МЧ. Через кривизну МЧ зменшується довжина шляху, на якому відбувається поглинання рентгенівських фотонів, і в діапазоні діаметрів D = 2–6 мкм відношення І_і/І_∞і може бути більше одиниці (на рис. 7.8 це проілюстровано залежністю, отриманою при ψ = 90°).

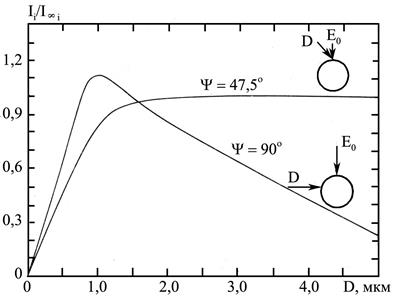
Рисунок 7.8 – Залежність відносної інтенсивності рентгенівського випромінювання атомів Si в Fe від діаметра МЧ. Швидке спадання інтенсивності І_і при ψ = 90° обумовлене аномальним поглинанням МЧ рентгенівського випромінювання

Закінчуючи питання про кількісний РМА, відмітимо декілька прикладних аспектів цієї проблеми. По-перше, в сучасних технологіях велике значення мають матеріали, отримані із порошків металів, неметалів, хімічних з’єднань. Важливою характеристикою порошків, яка визначає фізико-хімічні та механічні властивості виробів із них, є хімічний і фазовий склад та характер розподілу фаз і компонент у виробі. У зв’язку з цим методи РЕМ і РМА, як методи неруйнівного контролю структури і складу матеріалів, використовуються на усіх стадіях отримання матеріалів порошкової металургії. Залежно від розміру частинок порошки умовно поділяють на такі класи: 0,001–0,1 мкм (ультрадисперсні); 0,1 – 10 мкм (тонкодисперсні); 10 – 200 мкм (середньодисперсні); 200 – 1000 мкм (крупнодисперсні). З точки зору РМА середньо- і крупнодисперсні порошки можна віднести до категорії масивних зразків, а для класифікації тонкодисперсних порошків необхідно вести додатковий аналіз. Оскільки при підготовці порошкових зразків їх пресують, розміщують у в’язкі середовища або закріплюють на металевих підкладках, то для них неможливо підготувати еталони у вигляді порошків і тому використовують масивні еталони. В силу різних причин метод трьох поправок неможливо використати при РМА порошків.

Свої особливості має РМА пористих матеріалів і біологічних об’єктів. Однак коло цих питань виходить за рамки даного посібника.