Метод трьох поправок

Метод трьох поправок знайшов широке застосування при дослідження металів і сплавів. Його запропонував у 1951 р. французький вчений Р. Кастен (R. Castaing) * у своїй дисертаційній роботі. В основу методу покладено запропоноване ним співвідношення

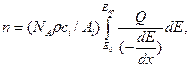(7.1)

де n – середнє число актів іонізації і-го елемента на один електрон; dE/dx – середні втрати енергії на відрізку dx; N_A – число Авагадро; А_і та с_і – атомна маса та концентрація і-го елемента; ρ – густина зразка; Е_кр – критична енергія збудження певної характеристичної (К, L чи М) рентгенівської лінії і-го елемента; Q – ймовірність іонізації певної електронної оболонки атомів зразка (іншими словами – переріз іонізації) електроном заданої енергії на одиничному шляху пробігу; (N_Aρc_i/A_i) – число атомів і-го елемента в одиниці об’єму (атомна концентрація); знак “мінус” враховує, що при dx > 0 енергія електрона зменшується (dE < 0).

Оскільки частина первинних електронів відбивається від поверхні зразка, то необхідно у співвідношення (7.1) ввести коефіцієнт відбиття R як відношення інтенсивності рентгенівського випромінювання зразка до інтенсивності, яка б випромінювалася за умови, що всі первинні електрони залишилися у зразку. Враховуючи, що середня інтенсивність рентгенівського випромінювання (І) і-го елемента на один первинний електрон пропорційна величині n (співвідношення (7.1)), то можна записати

_________________________

* У 1950-х рр. в лабораторії Р. Кастена проходив стажування В.Т. Черепін (зараз чл.-кор. НАН України, співробітник ІФМ НАН України) – провідний фахівець України з розробки спектральних приладів і методів аналізу і, зокрема, методу вторинно-іонної мас-спектрометрії.

(7.2)

де Е₀ – енергія первинного електрона; С – стала величина.

Для отримання аналітичного зв’язку між рівнянням (7.2) і концентрацією с_і Р. Кастен запропонував метод еталона (інша назва – зразок порівнювання). Суть методу полягає в тому, що вимірюється інтенсивність рентгенівського випромінювання одним і тим самим детектором від зразка із невідомою концентрацією і-го елемента (І_і) та еталона (І_0і), причому енергія Е₀, струм електронного пучка і кут виходу рентгенівського випромінювання підтримуються постійними. Якщо взяти відношення І_і до І_0і, то співвідношення (7.2) перепишеться таким чином:

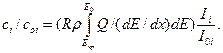
(7.2′)

У першому наближенні, коли еталон складається із чистого і-го елемента, величини R, ρ, Q та dE/dx можна вважати однаковими для невідомого зразка й еталона. В такому разі (7.2′) перетворюється до простого вигляду

(7.3)

Це перше наближення Р. Кастена, яке можна використовувати для попередньої оцінки хімічного складу. Для отримання більш коректного результату необхідно ввести поправки на різницю величин R, ρ, Q та dE/dx у зразку й еталоні та на поглинання рентгенівського випромінювання у твердому тілі.

У методі трьох поправок була здійснена корекція для деяких ефектів:

– різниці в розсіюванні та гальмуванні електронів у досліджуваному зразку та еталоні (фактор Z_i);

– поглинання рентгенівського випромінювання атомами з масою А_і (фактор А_і);

– поправка на флуоресценцію (фактор F_i).

Із урахування цих поправок співвідношення (7.3) можна переписати таким чином:

(7.4)

Найбільш складним питанням у методі трьох поправок є розрахунок цих поправок. Проблема полягає в тому, що зазначені фактори залежать від багатьох параметрів. Наприклад, фактор атомного номера обумовлюється явищами відбиття і гальмування електронів. Загалом, якщо не вводити поправку на ці ефекти, то при МРА легких елементів у матриці важких елементів отримуються дуже завищені значення концентрації, а при аналізі важких елементів у матриці з легкого елемента, навпаки, дуже занижені значення концентрації.

З великою точністю співвідношення для Z_i можна записати таким чином:

де та 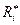- коефіцієнти зворотного розсіювання для і-го елемента в еталоні й зразку відповідно; 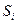та - гальмівна здатність електрона в еталоні й зразку.

Наведене співвідношення майже завжди дає правильне значення Z_i, але на його величину значно впливає різниця між середніми атомними номерами зразка та еталона (збільшення цієї різниці призводить до збільшення величини Z_i). Крім цього, похибка визначення Z_i залежить від величини прискорюючої напруги електронів (для досягнення найбільшої точності необхідно використовувати значні напруги).

На величину поправки А_і впливають три основні фактори: енергія Е₀, кут виходу рентгенівського випромінювання і масовий коефіцієнт поглинання (μ/ρ)_і. Для зведення до мінімуму величини А_і необхідно вести аналіз при малих значеннях (μ/ρ)_і та кута виходу, а також при відносно малих прискорюючих напругах первинних електронів. Єдиний спосіб зменшення поправки А_і полягає у виборі еталона, в якого .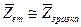

Поправка на флуоресценцію пов’язана як із характеристичним, так і гальмівним рентгенівським випромінюванням.

Перший ефект проявляє себе, якщо Е характеристичного піка j-елемента більше Е_кр і-го елемента. Поправка F_i буде абсолютно незначною, якщо Е – Е_кр > 5 кеВ, але в інших випадках необхідно робити поправку на флуоресценцію, оскільки енергія рентгенівського випромінювання від атомів j-го елемента обумовить збільшення інтенсивності рентгенівського випромінювання порівняно лише з електронним збудженням. Збільшення інтенсивності рентгенівського випромінювання атомами і-го елемента за рахунок флуоресцентного випромінювання атомів j-го елемента можна розрахувати за допомогою співвідношення

де та - інтенсивності і-го елемента під дією флуоресценції j-го елемента та інтенсивність випромінювання під дією електронів відповідно; с_j – концентрація атомів j-елемента; Y₀ – Y₃ – відомі функції; P_ij – фактор, який враховує пік виникаючої флуоресценції (наприклад, якщо К або L лінії збуджують відповідно К або L лінії, то P_ij=1; для L–К або К–L – флуоресценцій P_ij=4,76 або 0,24 відповідно).

Незважаючи на дуже складний вид функції Y₀ – Y₃, їх завжди можна розрахувати до числа, що відкриває можливість визначити величину / та F_i.

Якщо здійснити порівняльний аналіз впливу трьох поправок, то якраз найменш важливою із них є поправка (F_i)_хв за рахунок характеристичного випромінювання, оскільки в реальній експериментальній ситуації c_j може бути дуже малою або вторинна флуоресценція може взагалі не відбуватися.

Другий ефект флуоресценції виникає за рахунок суцільного (гальмівного) рентгенівського випромі-нювання, кванти якого мають енергію, достатню для збудження будь-якого характеристичного випромінювання в діапазоні енергій від Е до Е_кр. Теоретичні дослідження свідчать про те, що розрахунок інтенсивності вторинного випромінювання, що збуджується суцільним спектром рентгенівського випромінювання, надзвичайно складний. Точний його розрахунок потребує значного обсягу програмного матеріалу. У зв’язку з цим були проведені дослідження, в яких випадках можна знехтувати поправкою (F_i)_св при РМА. Було встановлено, що у багатьох випадках поправкою (F_i)_св можна знехтувати. Зокрема, мова йде про аналіз важких елементів у легкій матриці (тобто важка компонента в оксидах); про те, що зміна прискорюючої напруги і похибка у визначенні кута виходу випромінювання не впливають на величину (F_i)_св; при с_i > 0,5, 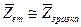та при великих кутах виходу випромінювання (F_i)_св також не відіграє істотної ролі.

Закінчуючи розгляд методу трьох поправок, відмітимо, що його можна застосувати до будь-якого класу зразків. Але при величині енергії рентгенівського випромінювання < 1 кеВ він дає результати зі значною похибкою. З цієї самої причини використання низькоенергетичних рентгенівських ліній забезпечує меншу точність, ніж у випадку високоенергетичних ліній.