ЛИНЕЙНОЕ УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА
Определение.Линейным уравнением первого порядка называется уравнение вида:  с непрерывными функциями
с непрерывными функциями 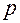 и
и 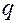 .
.
Будем искать общее решение методом И.Бернулли в виде произведения двух новых неизвестных функций: 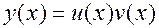 , что дает определенную свободу в выборе одного из множителей, позволяя придать ему необходимый для дальнейшего вид. Тогда
, что дает определенную свободу в выборе одного из множителей, позволяя придать ему необходимый для дальнейшего вид. Тогда 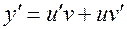 . Подставляя эти выражения в исходное уравнение, получим:
. Подставляя эти выражения в исходное уравнение, получим:
 .
.
Группируя слагаемые с 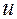 , получаем:
, получаем: 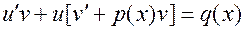 .
.
Потребуем от функции 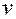 , чтобы множитель в квадратных скобках при
, чтобы множитель в квадратных скобках при 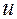 тождественно обращался в нуль:
тождественно обращался в нуль:
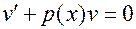 (10)
(10)
Уравнение (10) является уравнением с разделяющимися переменными. Найдем его частное решение 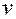 (без произвольной постоянной):
(без произвольной постоянной):
(10)  .
.
Интегрируем обе части:
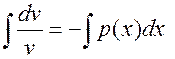 ;
; 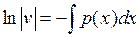 ;
; 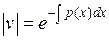 ;
;
выбираем в качестве частного решения функцию 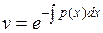 (здесь символом неопределенного интеграла обозначена какая-либо первообразная функции
(здесь символом неопределенного интеграла обозначена какая-либо первообразная функции 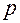 ) .
) .
Теперь подстановка найденной функции 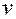 в (10) дает уравнение с разделяющимися переменными относительно
в (10) дает уравнение с разделяющимися переменными относительно 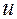 :
:
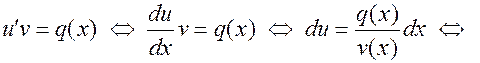
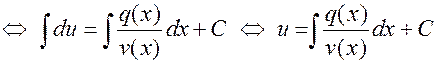 .
.
В итоге получаем общее решение:
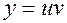 ;
;
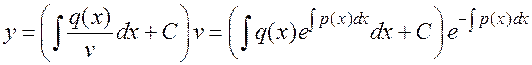 . (11)
. (11)
Хотя при решении линейного уравнения можно сразу выписывать общий интеграл по формуле (11), представляется полезным проследить на примере всю цепочку выкладок, приводящих к (11).
Пример.Рассмотрим линейное уравнение:
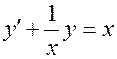
на интервале 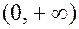 с начальными условиями
с начальными условиями 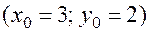 .
.
Здесь 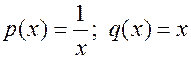 . Полагаем:
. Полагаем:
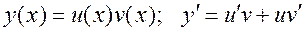 .
.
Подставляем в уравнение выражения для 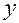 и
и 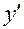 :
:
 .
.
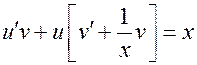 . (12)
. (12)
Накладываем на 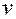 условие:
условие: 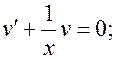 тогда
тогда

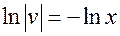 , и можно выбрать
, и можно выбрать 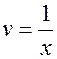 . Подставляем
. Подставляем 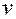 в (12) и учитываем, что, в соответствии с выбором функции
в (12) и учитываем, что, в соответствии с выбором функции 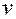 , выражение в квадратных скобках тождественно равно нулю:
, выражение в квадратных скобках тождественно равно нулю:
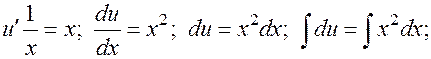
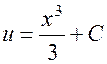 .
.
Функция
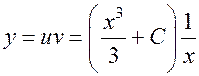
является общим решением.
Найдем частное решение задачи Коши. Подставим для этого начальные условия в общее решение и найдем соответствующее значение константы 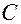 :
:
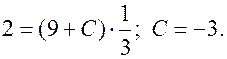
Подставив найденное значение 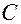 в общее решение, получаем решение задачи Коши:
в общее решение, получаем решение задачи Коши:
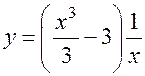 .
.
Дата добавления: 2015-05-08; просмотров: 757;
