Свойства решений однородного линейного уравнения
Из свойств производной следует, что для любых функций 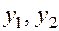 и любых вещественных чисел
и любых вещественных чисел 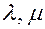 :
:
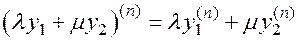 .
.
Обозначим левую часть уравнений (14) и (15) через 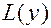 :
:
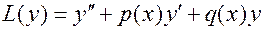 .
.
Тогда эти уравнения принимают вид 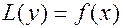 и
и 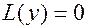 соответственно. При этом
соответственно. При этом
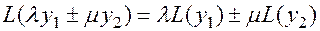 ,
,
Теорема 3: Если функции 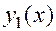 и
и 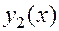 являются решениями однородного линейного уравнения (15), то функция
являются решениями однородного линейного уравнения (15), то функция  также является его решением.
также является его решением.
Доказательство. Пусть 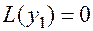 и
и  . Тогда
. Тогда
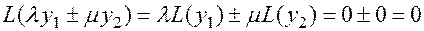 . ▄
. ▄
Дата добавления: 2015-05-08; просмотров: 735;
