Структура общего решения неоднородного линейного уравнения.
Определение.Для линейного уравнения второго порядка
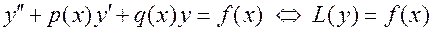
соответствующим однородным уравнением называется уравнение
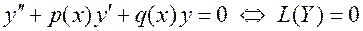 .
.
Можно доказать, что относительно структуры общего решения неоднородного линейного уравнения справедлива следующая
Теорема 4.Общее решение неоднородного уравнения 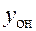 представимо суммой общего решения соответствующего однородного уравнения
представимо суммой общего решения соответствующего однородного уравнения 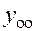 и частного решения неоднородного уравнения
и частного решения неоднородного уравнения 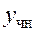 :
: 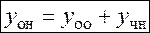 .
.
Доказательство. Поскольку
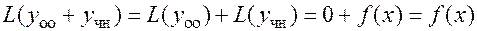 ,
,
то 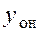 действительно является решением неоднородного уравнения. Далее,
действительно является решением неоднородного уравнения. Далее, 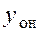 зависит от произвольных постоянных
зависит от произвольных постоянных 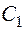 и
и  , поскольку от них зависит функция
, поскольку от них зависит функция 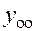 .
.
Остается убедиться, что за счет выбора значений этих постоянных можно получить решение задачи Коши с любыми наперед заданными начальными условиями 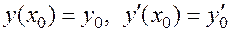 . Поскольку
. Поскольку 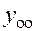 — общее решение соответствующего однородного уравнения, то можно выбрать такие значения постоянных
— общее решение соответствующего однородного уравнения, то можно выбрать такие значения постоянных 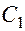 и
и 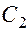 , при которых
, при которых
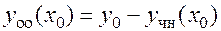 ;
;
и
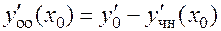 .
.
Тогда для функции 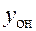 при этих значениях
при этих значениях 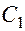 и
и 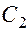 :
:
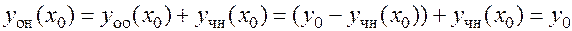
и
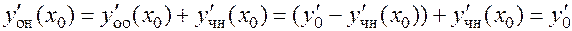 . ▄
. ▄
Дата добавления: 2015-05-08; просмотров: 770;
