МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНЫХ ПОСТОЯННЫХ
(МЕТОД ЛАГРАНЖА)
Рассмотрим линейное неоднородное уравнение второго порядка с постоянными коэффициентами
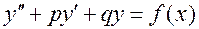 .
.
Согласно изложенному в п. 8.4, его общее решение представимо в виде 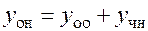 . Общее решение соответствующего однородного уравнения записывается в виде
. Общее решение соответствующего однородного уравнения записывается в виде
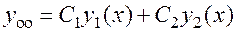 . (22)
. (22)
с произвольными постоянными 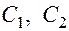 . Функции
. Функции 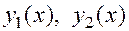 , в зависимости от корней характеристического уравнения, имеют вид:
, в зависимости от корней характеристического уравнения, имеют вид:
(а) 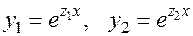 — при
— при 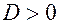 ,
, 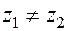 ;
;
(б) 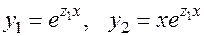 — при
— при 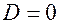 ,
, 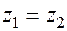 ;
;
(в) 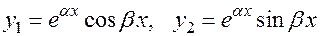 — при
— при 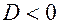 ,
,
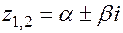 .
.
Таким образом, остается найти какое-либо частное решение исходного неоднородного уравнения 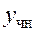 . Метод вариации произвольных постоянных, предложенный Лагранжем, предполагает отыскание
. Метод вариации произвольных постоянных, предложенный Лагранжем, предполагает отыскание 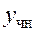 в виде, аналогичном (22), но уже с переменными множителями при
в виде, аналогичном (22), но уже с переменными множителями при 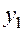 и
и 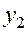 :
:
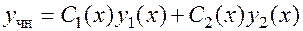 .
.
Здесь 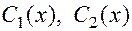 – подлежащие определению неизвестные функции.
– подлежащие определению неизвестные функции.
Вычислим производные частного решения (аргумент 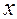 для краткости опускаем):
для краткости опускаем):
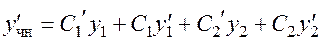 .
.
Наложим на функции 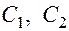 условие:
условие:
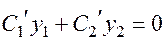 ; (23)
; (23)
тогда
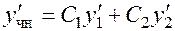 .
.
Дифференцируем повторно:
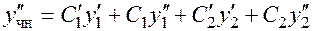 .
.
Подставим выражения для 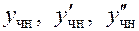 в исходное уравнение и сгруппируем по отдельности слагаемые с
в исходное уравнение и сгруппируем по отдельности слагаемые с 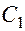 и с
и с 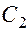 :
:
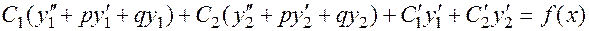 .
.
Множители при 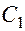 и
и 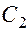 равны тождественно нулю, поскольку функции
равны тождественно нулю, поскольку функции 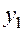 и
и 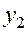 являются решениями однородного уравнения, так что
являются решениями однородного уравнения, так что
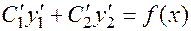 . (24)
. (24)
Соотношения (23) и (24) дают систему двух уравнений относительно неизвестных 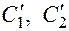 :
:
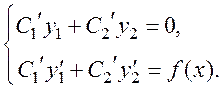 (25)
(25)
Решая эту систему, получим выражения для 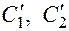 через уже известные функции
через уже известные функции 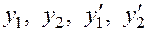 , после чего сами функции
, после чего сами функции 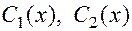 находятся интегрированием.
находятся интегрированием.
В качестве итога сформулируем алгоритм решения неоднородного уравнения методом вариации произвольных постоянных:
1. Решение соответствующего однородного уравнения, получение функций 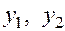 .
.
2. Запись общего решения соответствующего однородного уравнения в виде 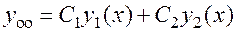 .
.
3. Вычисление производных 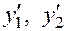 .
.
4. Запись системы (25) для отыскания 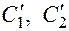 .
.
5. Решение системы, получение функций 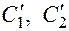 .
.
6. Нахождение каких-либо первообразных 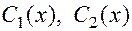 ин-
ин-
тегрированием функций 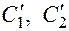 .
.
7. Запись частного решения неоднородного уравнения в виде
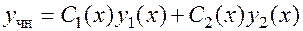 .
.
8. Запись общего решения неоднородного уравнения:
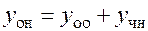 .
.
Пример. Решим методом вариации произвольных постоянных уравнение 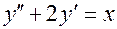 . Следуя алгоритму, последовательно получаем:
. Следуя алгоритму, последовательно получаем:
1. 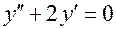 ;
; 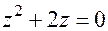 ;
; 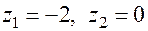 ;
;
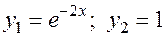 .
.
2. 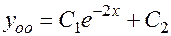 .
.
3. 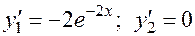 .
.
4. 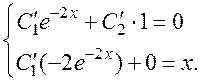
5. 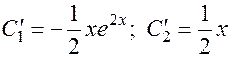 .
.
6. Интегрируя по частям, имеем:
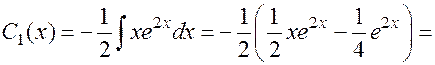
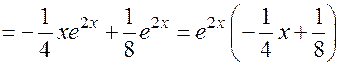 .
.
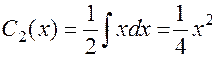 .
.
7. 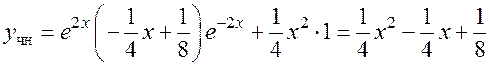 .
.
8. 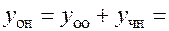
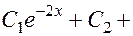
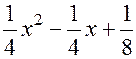 .
.
Дата добавления: 2015-05-08; просмотров: 1742;
