МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
Определение. Уравнением с разделенными переменными называетсядифференциальное уравнение первого порядка вида
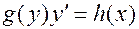 , (4)
, (4)
с непрерывными функциями 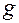 и
и 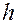
Смысл этого термина заключается в том, что переменные 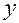 и
и 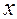 разделены по разным частям равенства (4).
разделены по разным частям равенства (4).
Напомним, что, согласно определению, дифференциал функции 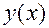 есть произведение производной на дифференциал независимой переменной:
есть произведение производной на дифференциал независимой переменной: 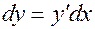 . Если умножить обе части равенства (4) на
. Если умножить обе части равенства (4) на 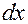 , получим:
, получим:
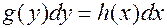 . (5)
. (5)
Это другой, более традиционный способ записи уравнения с разделенными переменными.
Теорема. Если в уравнении (5) функции 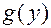 и
и 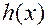 имеют первообразные
имеют первообразные 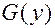 и
и 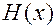 , то общий интеграл уравнения имеет вид:
, то общий интеграл уравнения имеет вид:
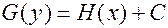 , (6)
, (6)
где 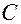 — произвольная постоянная.
— произвольная постоянная.
Замечание. Если для обозначения первообразных использовать символ неопределенного интеграла, то общий интеграл записывается в виде:
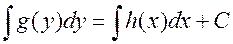 . (7)
. (7)
Доказательство. Опуская доказательство того, что уравнение (6) действительно задает неявную функцию 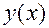 , убедимся, что
, убедимся, что 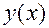 удовлетворяет уравнению (4). Для этого продифференцируем по
удовлетворяет уравнению (4). Для этого продифференцируем по 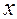 равенство (6), применяя для левой части правило производной сложной функции с промежуточной переменной
равенство (6), применяя для левой части правило производной сложной функции с промежуточной переменной 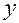 :
:
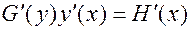 ,
,
или, учитывая, что 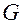 и
и 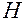 первообразные для
первообразные для 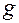 и
и 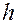 :
:
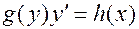 .
.
Остается убедиться, что за счет выбора значения произвольной постоянной 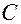 можно обеспечить выполнение любых начальных условий
можно обеспечить выполнение любых начальных условий 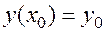 . Подставляя начальные условия в (6), получаем:
. Подставляя начальные условия в (6), получаем:
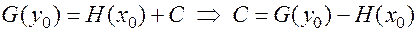 . ▄
. ▄
Примеры. 1. Для уравнения 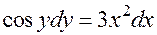 найдем общий интеграл и частный интеграл для начальных условий
найдем общий интеграл и частный интеграл для начальных условий 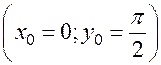 . Имеем:
. Имеем:
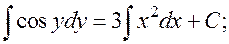
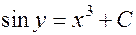 —
—
это общий интеграл.
Подставим теперь в общий интеграл начальные условия и найдем соответствующее значение константы 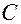 :
:
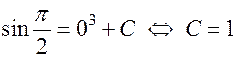 .
.
Следовательно, частный интеграл, дающий решение задачи Коши, имеет вид:
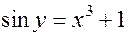 .
.
2. Рассмотрим уравнение 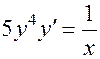 с начальными условиями
с начальными условиями 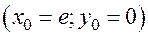 . Умножая обе части уравнения на
. Умножая обе части уравнения на 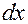 и затем интегрируя, получаем:
и затем интегрируя, получаем:
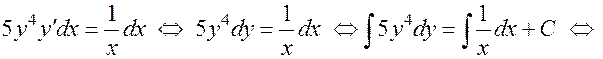
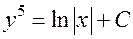 – это общий интеграл. Выражая отсюда явно
– это общий интеграл. Выражая отсюда явно 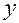 через
через 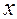 и
и 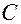 , получаем общее решение:
, получаем общее решение: 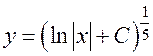 . Подстановка начальных условий в общее решение дает:
. Подстановка начальных условий в общее решение дает: 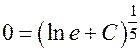 , так что
, так что 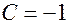 . Следовательно, функция
. Следовательно, функция 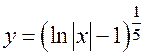 является решением задачи Коши.
является решением задачи Коши.
Определение. Уравнением с разделяющимися переменными называетсядифференциальное уравнение первого порядка вида
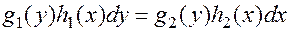 , (8)
, (8)
с непрерывными функциями 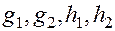 .
.
В этом уравнении каждая из частей является произведением двух множителей, один из которых зависит только от 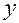 , а другой – только от
, а другой – только от 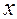 .
.
От этого уравнения легко перейти к уравнению с разделенными переменными, деля обе части на произведение 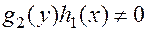 («разделяя переменные»):
(«разделяя переменные»):
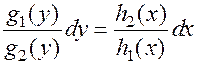 .
.
Примеры. 1. 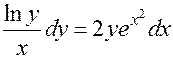 . Обе части разделим на
. Обе части разделим на 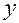 и умножим на
и умножим на 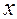 :
: 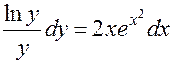 . Интегрируем:
. Интегрируем:
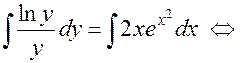
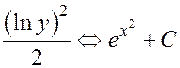 —
—
общий интеграл.
2. 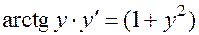 ; начальные условия:
; начальные условия: 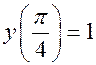 . Записываем производную
. Записываем производную 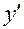 как отношение дифференциалов:
как отношение дифференциалов:
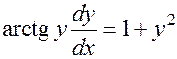 .
.
Обе части умножим на 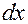 , разделим на
, разделим на 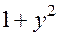 и проинтегрируем:
и проинтегрируем:
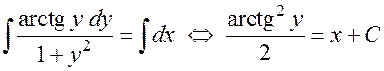 —
—
общий интеграл. Найдем теперь частный интеграл, удовлетворяющий начальным условиям. Подставляя начальные условия в полученное уравнение, имеем:
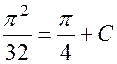 ;
; 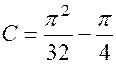 .
.
Следовательно, частный интеграл, дающий решение задачи Коши, имеет вид:
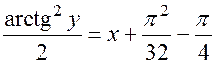 .
.
Дата добавления: 2015-05-08; просмотров: 894;
