Линейное пространство матриц

Матрицей n ´ m называется прямоугольнаятаблица 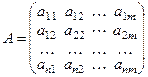, где а_ij – принадлежат некоторому числовому полю K и называются элементами матрицы A или матричными элементами А. Иногда пишут А_nm. Здесь индексы определяют размеры матрицы А (1^й – количество строк, 2^й – количество столбцов). Матрицы А и В называются равными (А = В), если их размеры совпадают и а_ij = b_ij.

На множестве матриц одинаковых размеров можно определить операцию сложения: C = A + B так, что c_ij = а_ij + b_ij, и операцию умножения на скаляр из внешнего поля К: D = a×A Û d_ij = a×а_ij.

1°. Множество матриц А_nm с так определенными операциями поэлементного сложения и умножения на скаляр образуют линейное пространство К_nm. Доказать самостоятельно.

При этом dimK_nm = n×m, а базис образуют матрицы E_ij , у каждой из которых элемент, стоящий на пересечении i-ойстрочки и j-ого столбца равен 1, а остальные элементы равны 0. Нейтральным элементом является матрица Q у которой все элементы равны 0.

Если у матрицы А_nm n = m ,то матрица А называется квадратной, а число n называют порядком этой матрицы. При этом если для еe элементов а_ij = а_ji – матрица называется симметрической (или симметричной), а если а_ij = –а_ji, то матрица называется кососимметрической (или кососимметричной).

2°. Всякая квадратная матрица может быть разложена в сумму симметрической и кососимметрической матрицы.

◀ Пусть матрица А_nm задана своими элементами: A_nm = (а_ij), i = 1, 2, …, n, j = 1, 2, …, m. Построим матрицы S_nm и 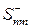элементы, которых связаны с а_ij следующими соотношениями 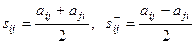. При этом s_ij = s_ji и 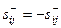. Т.е. матрицы S_nm и 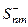соответственно симметричная и кососимметричная. Кроме того

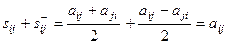, т.е. А = S + . ▶

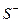3°. Множество симметричных (кососимметричных) матриц порядка n образуют линейное пространство. Самостоятельно установите базис и размерность этих пространств.