Линейные многообразия

Пусть L – подпространство V, x₀ÎV.

Множество M = {x | x = x₀ + y, yÎL} называется линейным многообразием в V.

О линейном многообразии M говорят, что оно параллельно подпространству L и обозначают M = x₀ + L.

Если x₀ÎL, то M º L и M является подпространством. Если x₀ÎV, но x₀ÏL то линейное многообразие подпространством не является.

29°. Линейное многообразие порождается сдвигом единственного L.

◀ Пусть M = x₀ + L и M = x¢₀ + L¢. Тогда "xÎM

x = x₀ + y = x¢₀ + y¢ Þ y = x¢₀ + y¢, где yÎL, y¢ÎL¢. Так как это верно для "yÎL, положим y = q. Получим y¢ = x₀ – x¢₀ и т.к. y¢ÎL¢ Þ x₀ – x¢₀ ÎL¢ . Тогда 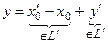Þ yÎL¢. Итак, если yÎL Þ yÎL¢ Þ L Ì L¢, аналогично L Ì L¢, тогда L = L¢ . ▶

Размерность линейного многообразия – это размерность соответствующего подпространства L, базис линейного многообразия – это базис соответствующего подпространства. Забавный нюанс – базис линейного многообразия самому многообразию, вообще говоря, не принадлежит.

1-мерное многообразие называется прямой, k-мерное многообразие называется k-мер-ной плоскостью, (n – 1)-мерное многообразие – называется гиперплоскостью (n = dimV).

§19. Действия с подпространствами

Пусть L₁ и L₂ – подпространства пространства V.

L = L₁ + L₂ Û L º {x | x=x₁ + x₂, x₁ÎL₁, x₂ÎL₂}

N = L₁∩L₂ Û N º {x | xÎL₁ Ù xÎL₂}

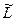= L₁∩L₂ Û 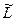º {x | xÎL₁ Ú xÎL₂}.

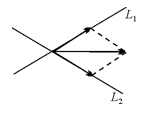
Отметим, что теоретико-множественное объединение подпрост-ранств подпространством, вообще говоря, не является. Рисунок иллюстрирует, что сумма векторов из L₁ + L₂ не всегда принадлежит L₁ + L₂ .

30°. L = L₁ + L₂ и N = L₁∩L₂, где L₁ и L₂ – подпространства также являются подпростран-

ствами.

◀ В доказательстве элементы подпространств L₁ и L₂ будем снабжать соответствующими индексами.

1) L = L₁ + L₂: "x, yÎL x + y = (x₁ + x₂) + ( y₁ + y₂ )= (x₁ + y₁) +(x₂ + y₂);

xÎL:ax = a(x₁+ x₂) = ax₁+ax₂; q_L = 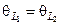= q_V ; (–х)=(–х)₁+(–х)₂ .

2) N = L₁∩L₂ : ; . ▶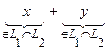

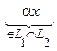31°. Формула Грасмана dim(L₁ + L₂) = dimL₁ + dimL₂ – dimL₁∩L₂.

◀ Пусть dimL₁∩L₂ = k, dimL₁ = k + l₁, dimL₂ = k + l₂. Докажем, что dim(L₁ + L₂) = k + l₁ + l₂.

Пусть 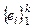базис в L₁∩L₂. Дополним его до базиса L₁: 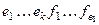и до базиса L₂: 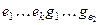. Покажем, что 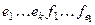, 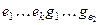базис в L₁ + L₂. Полнота:

x = x₁ + x₂ = = .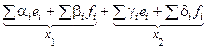

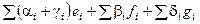Линейная независимость (от противного).

Пусть a₁e₁ + … + a_ke_k + b₁f₁ + … + 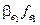+ g₁g₁ + … + 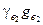= q;

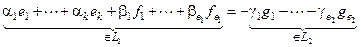
Из последнего равенства следует, что векторы стоящие в его левой и правой частях принадлежат L₁∩L₂ . Тогда уÎL₁∩L₂ можно записать в виде: y = d₁e₁ + … + d_ke_k.Сравнивая y = a₁e₁ + … + a_ke_k + b₁f₁ + … + 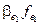с y = d₁e₁ +… + d_ke_k, в силу единственности разложения у, заключаем, что a₁ = d₁, a₂ = d₂, …, a_k = d_k; b₁ = b₂ = … = 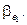Подставляя b_i= 0 в (*) получаем a₁e₁ + … + a_ke_k + g₁g₁ + …+ 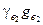= q и, в силу линейной независимости векторов e₁, е₂, …, e_k, g₁, g₂,…, 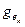получаем: a₁ = a₂ =… = a_k = g₁ =… = 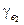= 0. ▶