Прямая сумма подпространств

Сумма L₁ + L₂ называется прямой суммой (и обозначается L₁⊕L₂), если представление х = х₁ + х₂(х₁ÎL₁, х₂ÎL₂) единственно для любого хÎV.

32°. Чтобы L₁+ L₂ была прямой необходимо и достаточно чтобы:

a) L₁∩L₂=q или б) dimV =dimL₁ + dimL₂.

◀ a) Необходимость. Пусть сумма L₁ + L₂ прямая и пусть $z₀ ¹ q и z₀ÎL₁∩L₂.Тогда х = х₁+ х₂ = (х₁+ z₀) + ( х₂– z₀)= х¢₁ + х¢₂ т.е. разложение x в сумму неоднозначно. Это противоречит тому, что сумма прямая.

Достаточность. L₁∩L₂ = q пусть х = х₁ + х₂и х = y₁ + y₂,

х – х = х₁– y₁ + х₂– y₂=q Þ 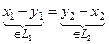Þ х₁– y₁ = y₂– х₂ÎL₁∩L₂ Þ х₁– y₁ = q и х₂– y₂=q, т.е. х₁= y₁ и х₂= y₂.

б)Необходимость. L₁⊕ L₂ Þ L₁∩L₂ = q, dimV =dimL₁ +dimL₂ – dimL₁∩L₂ =dimL₁ +dimL₂.

Достаточность. Если dimV = dimL₁+dimL₂Þ dimL₁∩L₂ = 0,т.е. L₁∩L₂ = q. ▶

Если V = L₁⊕L₂ Þ "xÎV существует единственное представление: х = х₁+ х₂ (х₁ÎL₁, х = L₂).

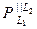При этом х₁называется проекцией х на L₁,параллельно подпространству L₂ ( х), а х₂называется проекцией х на L₁,параллельно подпространству L₁ ( 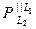х).

Подпространство L₂ называется дополнением L₁ к V и наоборот.

33°. "L₁ÌV существует L₂такое, что L₁⊕L₂ = V. Доказать самостоятельно.

34°. Если L₁⊕L₂ = V иdimV = n,dimL₁= k, то dimL₂ = n – k .

Доказать самостоятельно. Величина dimV – dimL₁= n – k называется коразмерностью подпрострарства L₁ и обозначается codimL₁ .