Дифференциальное уравнение свободных колебаний.

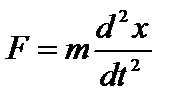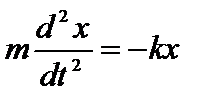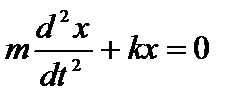Рассмотрим свободные колебания, происходящие в системе с одной степенью свободы. Пусть тело массой т укреплено на пружине, упругость которой k (пружинный маятник, рис.18.1). В отсутствие сил трения на тело, выведенное из положения равновесия, действует упругая сила пружины F= –kx. Тогда по второму закону динамики имеем: или . (1)

Если ввести обозначение , то уравнение (1) можно переписать в следующем виде:

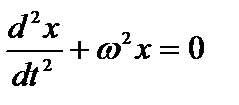(2)

Это и есть дифференциальное уравнение свободных колебаний с одной степенью свободы. Его решением является функция вида 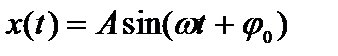. Величина 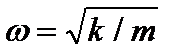является циклической частотой колебаний. Период колебаний пружинного маятника:

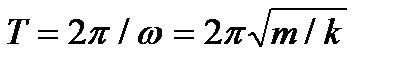(3).

Математический маятник. Это модель, в которой вся масса сосредоточена в материальной точке, колеблющейся на невесомой и недеформируемой нити (рис.18.2). При отклонении материальной точки от положения равновесия на малый угол a, такой, чтобы выполнялось условие 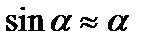, на тело будет действовать возвращающая сила. 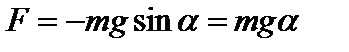Знак минус указывает, что сила направлена в сторону, противоположную смещению. Так как 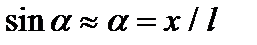, то сила равна 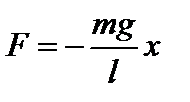. Сила пропорциональна смещению, следовательно, под действием этой силы материальная точка будет совершать гармонические колебания. Обозначим 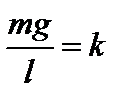, где 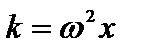, имеем: 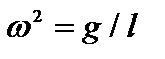или 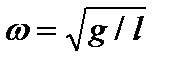. Отсюда период колебаний математического маятника: .