Фазовая и групповая скорость.
Процесс распространения колебаний в среде называется волновым процессом (или волной). Все разнообразие волн в природе и технике подразделяют на два типа: волны механические (упругие) и электромагнитные.
Упругими (или механическими) волнами называются механические возмущения, распространяющимися в упругой среде.
Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространения. Поперечные волны возникают при деформациях сдвига. Поэтому в жидкой и газообразной средах возникают только продольные волны.
При распространении колебаний в среде частицы не перемешаются вместе с волной, а лишь колеблются около своих положений равновесия. Поступательно перемещаются лишь фаза и энергия колебаний.
Графически волну изображают так же, как и колебания (рис.21.1).
 Геометрическое место точек, колеблющихся в одинаковых фазах, называется волновой поверхностью. В зависимости от формы волновой поверхности различают сферические, плоские, цилиндрические волны. Геометрическое место точек, до которых доходят колебания с одинаковой фазой к некоторому моменту времени t, называется фронтом волны. Фронт волны является частным случаем волновой поверхности.
Геометрическое место точек, колеблющихся в одинаковых фазах, называется волновой поверхностью. В зависимости от формы волновой поверхности различают сферические, плоские, цилиндрические волны. Геометрическое место точек, до которых доходят колебания с одинаковой фазой к некоторому моменту времени t, называется фронтом волны. Фронт волны является частным случаем волновой поверхности.
Расстояние, на которое определенная фаза распространяется за один период колебания, называется длиной волны l. Из рисунка видно, что l – это наименьшее расстояние между точками, колеблющимися в одинаковых фазах.
Скорость распространения волны (фазовая скорость). Фазовая скорость –равна скорости перемещения в пространстве точек поверхности, соответствующей любому фиксированному значению фазы. 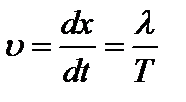 (1).
(1).
Волна, распространяющаяся в пространстве от какого-либо источника называется бегущей волной. Уравнение бегущей волны 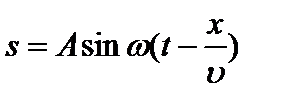 (2).
(2).
Для характеристики волн используется волновое число k, характеризующее скорость изменения фазы в пространстве 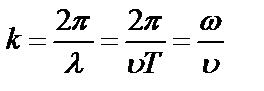 (3).
(3).
Учитывая (3), уравнение (2) примет вид: 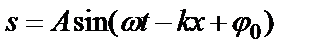 (4).
(4).
Уравнение волны, распространяющейся вдоль отрицательного направления оси 0Х отличается от (3) знаком члена kx.
Из условия 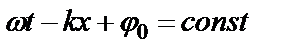 получаем выражение для фазовой скорости:
получаем выражение для фазовой скорости: 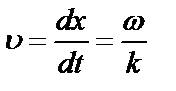 .
.
Дата добавления: 2015-04-01; просмотров: 1373;
