Решение. Так как дополнительные краевые условия аналогичны предыдущему примеру, вновь имеем , но, учитывая, что составим систему (56):
Так как дополнительные краевые условия аналогичны предыдущему примеру, вновь имеем  , но, учитывая, что
, но, учитывая, что 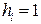 составим систему (56):
составим систему (56):
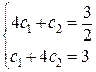
Решение этой системы будет
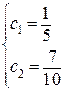
Значения коэффициентов 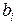 ,
, 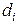 :
:
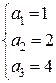
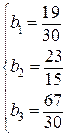

Таким образом, можно считать сплайн-интерполяцию построенной в виде
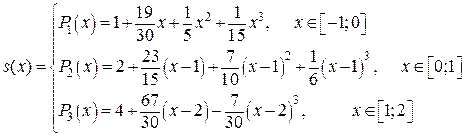
Для нахождения значения интерполирующей функции в заданной точке 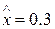 заметим, что
заметим, что 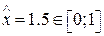 , и поэтому используем многочлен
, и поэтому используем многочлен 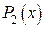 :
: 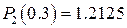 .
.
|

Сравнивая примеры 7 и 8 обратим внимание на следующее: погрешность в последнем явно меньше. Связано это в первую очередь с тем, что интервал выбран в два раза меньше. Можно показать, для случая равноотстоящих узлов
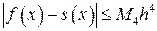
где 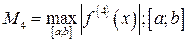 - промежуток интерполяции.
- промежуток интерполяции.
Интерполяция сплайнами сопряжена с немалым объемом вычислительной работы по сравнению с другими видами интерполяции. Однако эта трудность легко решается с помощью ЭВМ.
[1] Термины «интерполяция» и «экстраполяция», впервые предложены в 1656 году английским математиком Джоном Уоллисом (J. Wallis), образованы от латинского “polire” – сглаживать, и различаются предлогами “inter” и “extra” – соответственно «между» и «внутри».
[2] Можно показать непосредственную связь между конечными разностями и производными, а именно  . Доказательство этого положения предоставляем читателю.
. Доказательство этого положения предоставляем читателю.
[3] Легко убедиться, что форма 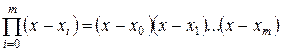 будет единственной, обращающейся в нуль в узловых точках.
будет единственной, обращающейся в нуль в узловых точках.
Дата добавления: 2015-04-25; просмотров: 869;

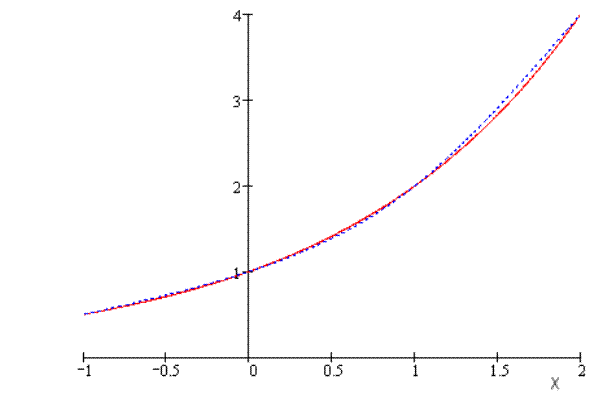 Рис. 3 График функции
Рис. 3 График функции 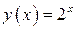 (сплошная кривая) и интерполирующий ее сплайн (пунктирная кривая).
(сплошная кривая) и интерполирующий ее сплайн (пунктирная кривая).