Решение. 1. Определяем кратность каждого узла и кратность интерполирующего многочлена
1. Определяем кратность каждого узла и кратность интерполирующего многочлена. Имеем: m=2; 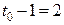 ;
; 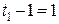 ;
; 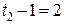 , откуда
, откуда 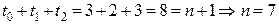 .
.
2. Общий вид многочлена Эрмита будет
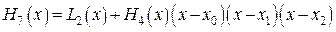 .
.
Интерполяционный многочлен Лагранжа находим по формуле (11)
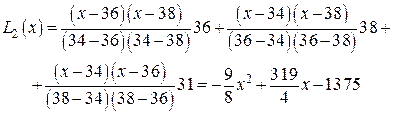
следовательно,
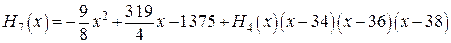 (*)
(*)
3. Так как максимальная кратность равна 2, то, дифференцируя дважды (*), получаем
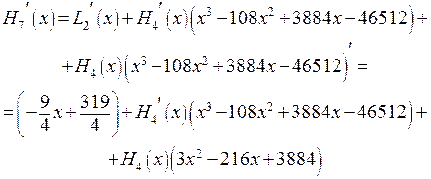
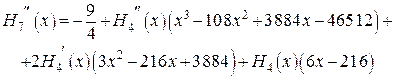
Из полученных формул получаем
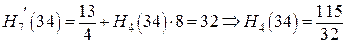
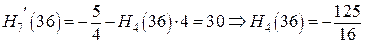
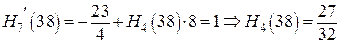
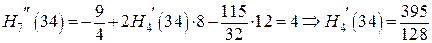
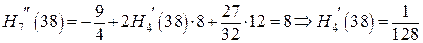
4. Сведем полученные данные о многочлене 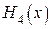 в таблицу
в таблицу
| i | xi | 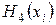
| 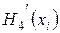
|
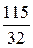
| 
| ||
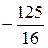
| |||
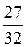
| 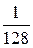
|
Определяем кратность каждого узла и уточняем кратность многочлена 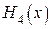 . Имеем: m=2;
. Имеем: m=2; 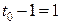 ;
; 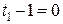 ;
; 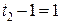 , откуда
, откуда 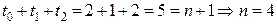 .
.
5. Общий вид многочлена Эрмита будет
 .
.
Новый интерполяционный многочлен Лагранжа находим по формуле (11):
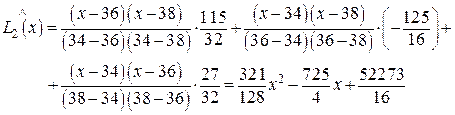
следовательно,
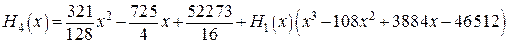 (**)
(**)
6. Так как максимальная кратность узлов таблицы многочлена 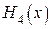 равна 1, то, дифференцируя один раз уравнение (**), получаем
равна 1, то, дифференцируя один раз уравнение (**), получаем
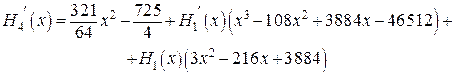
и по двум точкам
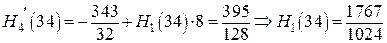
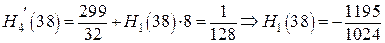
многочлен  определяется таблицей
определяется таблицей
| i | xi | 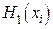
|
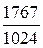
| ||
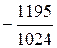
|
восстанавливается линейной интерполяцией (10)

Подставляя полученное выражение в (**), получаем для искомого многочлена
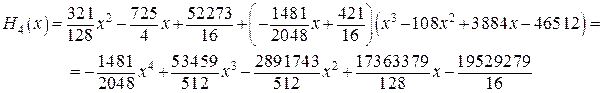
Наконец, подставляя последнее выражение в исходное (*), находим интерполирующий функцию 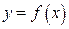 полином Эрмита
полином Эрмита
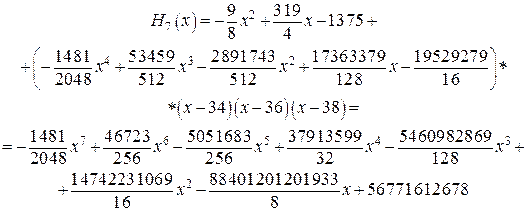
7. Непосредственной проверкой (проверьте!), убеждаемся, что полученный многочлен 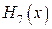 действительно является интерполирующим для функции
действительно является интерполирующим для функции 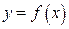 , т.е. удовлетворяет условию задачи. Кроме того, имеем возможность найти неопределенное в условии значение
, т.е. удовлетворяет условию задачи. Кроме того, имеем возможность найти неопределенное в условии значение 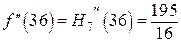 .
.
Дата добавления: 2015-04-25; просмотров: 1059;
