Уравнение Бернулли. Профессор Казанского университета И.С

Профессор Казанского университета И.С. Громека преобразовал уравнения Эйлера в иную форму, соответствующую идеальной, несжимаемой, однородной жидкости. Массовые силы для большинства практических задач соответствовали силе тяжести. Режим движения данной жидкости был стационарным, т.е. 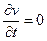и безвихревой.

Умножим каждое из уравнений Эйлера последовательно на 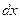, , 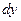и .

Система дифференциальных уравнений Л. Эйлера для идеальной движущейся жидкости на координатные оси

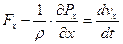
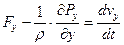
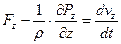
Раскроем скобки и сгруппируем, получим:

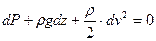(5.7)

Это выражение называют уравнением Бернулли в дифференциальной форме. При условии 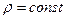(для несжимаемой жидкости) интегрирование его дает:

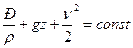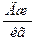, (5.8)

Этот интеграл называют интегралом Бернулли, из уравнения (5.8.) следует, что сумма удельной кинетической 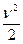, удельной потенциальной 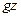энергии и удельной работы сил давления 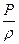- есть величина постоянная.

Для того, чтобы записать интеграл Бернулли в размерностях давления, умножим обе части (5.8) на плотность 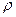и получим

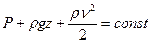(5.9)

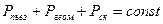(5.10)

где:

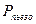- удельная потенциальная энергия единицы объема жидкости, Па.

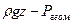геометрическое давление - удельная энергия положения единицы объема жидкости, Па.

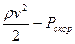скоростное давление - удельная кинематическая энергия единицы объема жидкости, Па.

Таким образом, уравнение Бернулли это частный случай закона сохранения энергии.