Дифференциальные уравнения движения вязкой жидкости Навье-Стокса

В 1822 году Клод Луи Навье получил уравнения движения вязкой жидкости путем преобразований уравнений движения, которые существенно усложняются. При движении вязкой жидкости в ней возникают не только нормальные, но и касательные напряжения, так как жидкость обладает способностью оказывать сопротивление относительно сдвигу своих слоев и частиц. Нормальные и касательные напряжения зависят не только от координат точек жидкости, но и от ориентации в пространстве площадки, на которую они действуют.

Представим движение жидкости в 2-х мерных координатах (рис.6.1)

Рис. 6.1 К выводу уравнения Навье-Стокса

Для вязкой жидкости справедлив закон трения Ньютона (2.7)

(6.1)

где 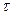- касательное напряжение, 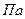; 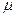- динамическая вязкость жидкости, .

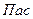Изменение касательных напряжений вдоль оси составит:

(6.2)

Подставляя в (6.2) значение 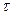, получим значение вязкостных напряжений вдоль оси :

(6.3)

Отнеся это изменение к единице объема жидкости, запишем:

(6.4)

где - кинематическая вязкость жидкости,

Дифференциальное уравнение движения вязкой несжимаемой жидкости вдоль оси :

(6.5)

Аналогично на другие оси:

(6.6)

Полученная система уравнений движения вязкой жидкости и носит название системы уравнений Навье-Стокса.

Три уравнения Навье-Стокса (6.6) плюс уравнение неразрывности

образуют замкнутую систему. Плотность и вязкость, входящие в них, считаются известными, а проекции массовых сил задаются условиями конкретной задачи.

С чисто математических позиций уравнения Навье-Стокса относится к классу нелинейных дифференциальных уравнений в частных производных второго порядка, и до настоящего времени, вследствие математических трудностей, не получено ни одного общего решения уравнений Навье-Стокса в их полном виде.