Правила построения ЧХ элементарных звеньев
При построении ЧХ некоторых звеньев можно использовать "правило зеркала": при к=1 ЛАЧХ и ЛФЧХ звеньев с обратными передаточными функциями зеркальны относительно горизонтальной оси. Так, на рис.5.6 изображены ЧХ идеального дифференцирующего (а) и идеального форсирующего звеньев (б).
Если к≠ 1, то передаточную функцию звена можно рассматривать как произведение W = kW1
где W1 - передаточная функция с к = 1.
При этом амплитуда вектора АФЧХ W(jω) при всех значениях φ должна быть увеличена в к раз, то есть А(ω) = kA1(ω).
Центр полуокружности АФЧХ апериодического звена будет находиться не в точке Р = 1/2, а в точке к/2. ЛАЧХ также изменится: L(ω) = 20lgA(ω) = 20lgkA1(ω) = 20lgk + 20lgA1(ω).
При к≠1 ЛАЧХ звена нужно поднять по оси ординат, не меняя ее формы, на 20lgк. На ЛФЧХ изменение к никак не отразится. Для примера на рис.5.7 приведены частотные характеристики апериодического звена при к=10 и Т = 1с. При этом ЛАЧХ апериодического звена с к = 1 поднята вверх на 20lg 10 = 20
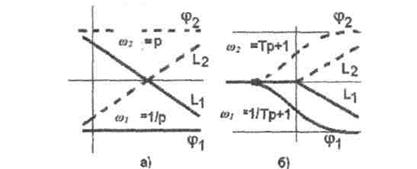
Рисунок 5.6 - ЧХ идеального дифференцирующего (а) и идеального форсирующего звеньев (б).
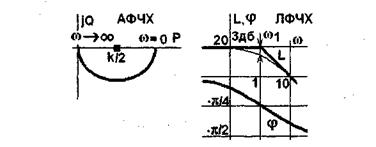
Рисунок 5.7 - Частотные характеристики апериодического звена при к = 10 и Т = 1с.
5.3. Частотные характеристики разомкнутых одноконтурных САУ
При исследовании и проектировании САУ часто используют АФЧХ, ЛАЧХ и ЛФЧХ разомкнутых систем. Это объясняется тем, что разомкнутые САУ более просто исследовать экспериментально, чем замкнутые. В то же время по ним можно получить исчерпывающую информацию о поведении данной САУ в замкнутом состоянии.
Любую многоконтурную САУ можно привести к одноконтурной. Разомкнутая одноконтурная САУ состоит из цепочки последовательно соединенных динамических звеньев. Зная передаточную функцию разомкнутой САУ, можно построить ее ЧХ. И наоборот, зная ЧХ разомкнутой САУ, снятую, например, опытным путем, можно найти ее передаточную функцию. Передаточная функция разомкнутой одноконтурной системы равна произведению передаточных функций отдельных звеньев:
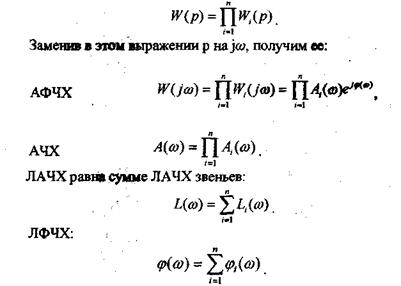
Таким образом, ЛАЧХ и ЛФЧХ разомкнутой САУ строят путем сложения ЛАЧХ и ЛФЧХ звеньев.
Для построения ЛАЧХ и ЛФЧХ рекомендуется следующий порядок:
1) раскладывают сложную передаточную функцию на множители, являющиеся передаточными функциями типовых динамических звеньев (порядок полиномов числителя и знаменателя не выше второго);
2) вычисляют сопрягающие частоты отдельных звеньев и строят асимптотические ЛАЧХ и ЛФЧХ каждого элементарного звена;
3) путем суммирования ЛАЧХ и ЛФЧХ звеньев строят результирующие ЧХ.
Лекция №6. «Законы регулирования и качество САР»
Дата добавления: 2015-04-21; просмотров: 1395;
