Инерционное звено первого порядка (апериодическое)

Уравнение динамики инерционного звена первого порядка:

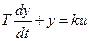
или

Тру + у = ки.

Это уравнение динамики, называемое иногда кривой разго­на, имеет вид экспоненты. Передаточная функция: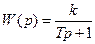

Переходная характеристика может быть получена с помощью формулы Хевисайда:

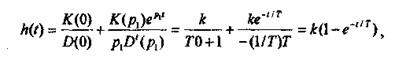
где p₁ = - 1/Т - корень уравнения D(p) = Тр + 1 - 0; D'(p₁) = Т.

Переходная характеристика имеет вид экспоненты (рис.4.5а), по которой можно определить передаточный коэффициент к, равный установившемуся значению h (ассимтота), и постоянную времени Т₀ по времени t, соответствующему точке пересечения касательной к кривой в начале координат с ее асимптотой. При достаточно больших Т₀ звено на начальном участке может рас­сматриваться как интегрирующее, при малых Т звено прибли­женно можно рассматривать как безынерционное.

Пример апериодического звена - четырехполюсник из сопротивления R и емкости С (рис.4.5б).

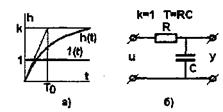
Рисунок 4.5 - Инерционное звено первого порядка (аперио­дическое).

У экспоненты есть свойство: если к любой ее точке провести касательную, а затем точку касания и точку пересечения касательной с асимптотой, к которой с течением времени приближается экспо­нента, спроецировать на ось времени t, то получают одну и ту же величину времени - «постоянную времени» Т₀, которая характе­ризует инерционные свойства объекта.

Ордината асимптоты, к которой стремится экспонента, по величине равна коэффициенту k в передаточной функции апе­риодического звена. Таким образом, по графику кривой разгона можно найти оба коэффициента- к и Т₀ впередаточной функции апериодического звена.

Еще одним примером реализации апериодического звена может быть установка - емкость равного по высоте сечения, ко­торая изображена на рис. 4.6. Бак на входе заполняет поток воды с расходом Q₁, из бака вытекает свободно поток с расходом Q₂

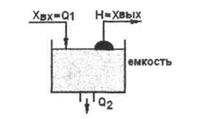
Рисунок 4.6 - Пример реализации апериодического звена при наполнении и истечении емкости с равным расходом.

Регулируемый параметр Х_вых - уровень Н в баке. При «еди­ничном скачке» Q₁ уровень Н повышается, увеличивается гидро­статическое давление, возрастает Q₂ и затем уровень Н стабили­зируется (экспонента приближается к асимптоте). Эта способ­ность самостоятельно восстанавливать равновесие, присущая объектам, аппроксимируемым апериодическим ТДЗ за счет наполнения или опорожнения энергии или вещества, называется самовыравниванием.

Самовыравнивание количественно определяется коэффици­ентом самовыравнивания, который равен обратной величине ко­эффициента к передаточной функции звена:

С= 1/ к

4.2.4. Инерционные звенья второго порядка

Уравнение инерционного звена второго порядка.

Т₁²р²у + Т₂ру + у = ки.

Передаточная функция: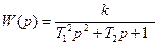

Решение уравнения зависит от соотношения постоянных вре­мени T₁ и Т₂, которое определяет коэффициент затухания

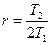
Можно записать

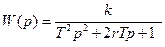
где Т=Т₁

Если г ≥1, то знаменатель W(p) имеет два вещественных корня р₁ и р₂ и раскладывается на два сомножителя: Тр₂ + 2rTp + 1 = Т₂ (р - p₁)(p – p₂).

Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.

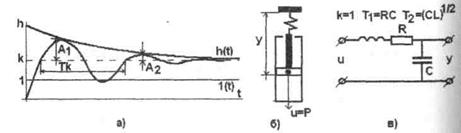
Рисунок 4.7 - Переходная характеристика инерционного звена второго порядка: А₁; А₂- амплитуда колебаний в разное время t; T_K- пери­од колебаний; l(t) - единичная функция; h(t) - переходная характеристика.

При r<1 корни полинома знаменателя W(p) комплексно со­пряженные: P_1,2 = α±j ω

Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс (рис.4.7а), с затуханием αи частотой ω(рис.4.7). Такое звено называется колебательным.

При r = 0 колебания носят незатухающий характер. Такое звено является частным случаем колебательного звена и называ­ется консервативным.

Примерами колебательного звена могут служить пружина, имеющая успокоительное устройство (рис,4.7б), электрический колебательный контур с активным сопротивлением (рис.4.7в) и т.п. Зная характеристики реального устройства можно, опреде­лить его параметры как колебательного звена. Передаточный ко­эффициент k равен установившемуся значению переходной функции.

4.2.5. Дифференцирующее звено

Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики идеального звена:

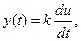или

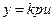
Здесь выходная величина пропорциональна скорости измене­ния входной величины. Передаточная функция: W(p)=kp.

При k=1 звено осуществляет чистое дифференцирование W(p) =p. Переходная характеристика: h(t) = k1΄V(t) = d(t).

Идеальное дифференцирующее звено реализовать невозмож­но, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала.

Его уравнение:

Тру + у = кТри

Передаточная функция: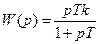

При малых Т звено можно рассматривать как идеальное диф­ференцирующее. Переходную характеристику можно вывести с помощью формулы Хевисайда:

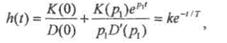
здесь p₁=-1/T - корень характеристического уравнения D(p) = Тр + 1=0; кроме того, D'(p₁) = Т.

По переходной характеристике, имеющей вид экспоненты (рис.4.8а), можно определить передаточный коэффициент k и постоянную времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости (рис.4.8б) и демп­фер, (рис.4.8.в). Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.

При подаче на вход единичного ступенчатого воздействия выход оказывается ограничен по величине и растянут во времени (рис.4.8а).

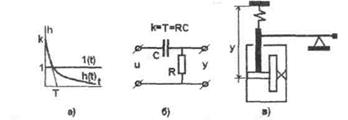
Рисунок 4.8 - Разновидность типовых дифференцирующих звеньев САР.