Понятие временных характеристик

Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию на типовые входные воздействия, которые наиболее полно отражают особенности ре­альных возмущений.

Это позволяет сравнивать отдельные элементы между собой с точки зрения их динамических свойств и, зная реакцию системы на типовые воздействия, можно судить о том, как она будет вести себя при сложных изменениях входной величины.

Наиболее распространенными типовыми воздействиями яв­ляются: ступенчатое, импульсное и гармоническое воздействия.

Любой сигнал u(t), имеющий сложную форму, можно разло­жить на сумму типовых воздействий u_i(t) и исследовать реакцию системы на каждую из составляющих, а затем, пользуясь прин­ципом суперпозиции, получить результирующее изменение вы­ходной величины y(t), суммируя полученные таким образом со­ставляющие выходного сигнала y_i(t).

Особенно важное значение в ТАУ придают ступенчатому воздействию

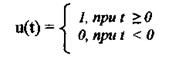
Все остальные воздействия могут быть сведены к нему. Так, например, реальный импульсный сигнал может быть представлен двумя ступенчатыми сигналами одинаковой величины, но проти­воположными по знаку, поданными один за другим через интер­вал времени Δt (рис.4.1.).

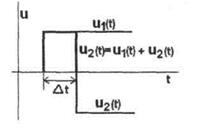
Рисунок 4.1 - Представление импульсного сигнала u (t) двумя ступенчатыми U₁(t) и U₂(t).

Зависимость изменения выходной величины системы от вре­мени при подаче на ее вход единичного ступенчатого воздейст­вия при нулевых начальных условиях называется переходной ха­рактеристикой и обозначается h(t).

Не менее важное значение в ТАУ уделяется импульсной пере­ходной характеристике ω(t), которая описывает реакцию систе­мы на единичное импульсное воздействие при нулевых началь­ных условиях. Единичный импульс физически представляет из себя, ограничивающий единичную площадь, очень узкий им­пульс, ширина которого стремится к нулю, а высота - к бесконеч­ности. Математически он описывается дельта - функцией d(t) = u'(t).

Переходная и импульсная переходная характеристики назы­ваются временными характеристиками. Каждая из них является исчерпывающей характеристикой системы и любого ее звена при нулевых начальных условиях. По ним можно однозначно опреде­лить выходную величину при произвольном входном воздейст­вии.

Зная передаточную функцию W(p) = K(p)/D(p), выражение для переходной функции можно найти из формулы Хевисайда:

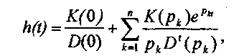
где р_к - корни характеристического уравнения D(p) = 0.

Взяв производную от переходной функции, можно получить выражение для импульсной переходной функции ω(t) = h'(t).