Передаточная функция

В ТАУ часто используют операторную форму записи диффе­ренциальных уравнений. При этом вводится понятие дифферен­циального оператора р = d/dt так, что dy/dt = ру, а рⁿ„ = dⁿ/dtⁿ. Это лишь другое обозначение операции дифференцирования. Обрат­ная дифференцированию операция интегрирования записывается как 1/р. В операторной форме исходное дифференциальное урав­нение записывается как алгебраическое:

а_ор^(п)у + a₁p^(n-1)y + ... +а_nу =(а_ор^(п) + a₁p^(n-1) + ... +а_n)y=(b_ор^(m) + b₁p^(m-1) + ... +b_m)u

Некоторые правила операционного исчисления математики применимы к операторной форме записи уравнения динамики. Так, оператор р можно рассматривать в качестве сомножителя без права перестановки, то есть ру≠ур

Его можно выносить за скобки и т.п. Поэтому уравнение ди­намики можно записать также в виде:

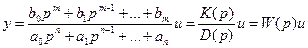
Дифференциальный оператор W(p) называют передаточной функцией. Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/u(t), поэтому ее еще называют динамическим коэффициентом усиления. В уста­новившемся режиме d/dt = 0, то есть p = 0, поэтому передаточная функция превращается в коэффициент передачи звена K=b_m/а_n

Знаменатель передаточной функции

D(p) = а_ор^(п) + a₁p^(n-1) + ... +а_n)

называют характеристическим уравнением. Его корни, то есть значения р, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами переда­точной функции

Числитель

К(р) =(b_ор^(m) + b₁p^(m-1) + ... +b_m)

называют операторным коэффициентом передачи. Его корни, при которых К(р) = 0 и W(p) = 0, называются нулями передаточ­ной функции.

Звено САУ с известной передаточной функцией называется динамическим звеном. Оно изображается прямоугольником, внутри которого записывается выражение передаточной функ­ции. То есть это обычное функциональное звено, функция кото­рого задана математической зависимостью выходной величины от входной в динамическом режиме.

Для звена с двумя входами и одним выходом должны быть записаны две передаточные функции по каждому из входов. Пе­редаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все осталь­ные характеристики. Она определяется только параметрами сис­темы и не зависит от входных и выходных величин.

Например, одним из динамических звеньев является интегра­тор. Его передаточная функция W_u(p) = 1/р. Схема САУ, состав­ленная из динамических звеньев, называется структурной.