Уравнение динамики САУ
Установившийся режим не является характерным для САУ. Обычно на управляемый процесс действуют различные возмущения, отклоняющие управляемый параметр от заданной величины. Процесс установления требуемого значения управляемой величины называется регулированием. Ввиду инерционности звеньев регулирование не может осуществляться мгновенно.
Рассмотрим САР, находящуюся в установившемся режиме, который характеризуется значением выходной величины у = у0. Пусть в момент t = 0 на объект воздействовал какой - либо возмущающий фактор, отклонив значение регулируемой величины у. Через некоторое время регулятор вернет САР к начальному состоянию (рис.3.11.). Если регулируемая величина изменяется во времени по апериодическому закону, то процесс регулирования называется апериодическим.
При резких возмущениях возможен колебательный затухающий процесс (рис.3.12а.). Существует и такая вероятность, что по истечении некоторого времени Тр в системе установятся незатухающие колебания регулируемой величины - незатухающий колебательный процесс (рис.3.12б). Последний вид - расходящийся колебательный процесс (рис.3.12в.).
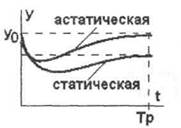
Рисунок 3.11 - Динамика статических и астатических САР после возмущения.
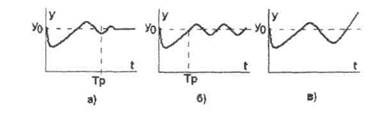
Рисунок 3.12 - Колебательные процессы в САР.
Таким образом, основным режимом работы САУ считается динамический режим, характеризующийся протеканием в ней переходных процессов. Поэтому второй основной задачей при разработке САУ является анализ динамических режимов работы САУ.
Поведение САУ или любого ее звена в динамических режимах описывается уравнением динамики y(t) = F(u, f, t), характеризующим изменение величин во времени. Как правило, это дифференциальное уравнение или система дифференциальных уравнений. Поэтому основным методом исследования САУ в динамических режимах является метод решения дифференциальных уравнений. Порядок дифференциальных уравнений может быть довольно высоким, то есть зависимостью связаны как сами входные и выходные величины u(t), f(t), y(t), так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так:
F(y,y',y", ...,у(п), и, и', и",..., и(m),f',f",f ...,f(к) = 0,
где: (y,y',y", ...,у(п), и, и', и",..., и(m),f',f",f ...,f(к) - соответственно: ' - первые; " - вторые; п, т, к- производные величин.
Дата добавления: 2015-04-21; просмотров: 1287;
