Структурные схемы в САУ

Обычно структурная схема САР состоит из отдельных эле­ментов, соединенных последовательно, параллельно или с помо­щью обратных связей. Каждый элемент имеет один вход, один выход и заданную передаточную функцию. Структурная схема САУ в простейшем случае строится из элементарных динамиче­ских звеньев. Но несколько элементарных звеньев могут быть за­менены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем.

Рассмотрим возможные способы преобразований.

1. Последовательное соединение - выходная величина пред­шествующего звена подается на вход последующего (рис. 3.13). При этом можно записать:

y₁=W₁y₀

y₂=W₂y₁

_……….

y_n=W_ny_n-1

y_n=W₁ W₂….W_ny₀

y_n=W_экв y₀

W_экв=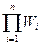

где п - число элементарных звеньев.

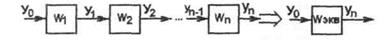
Рисунок 3.13 - Последовательное соединение звеньев САУ.

То есть цепочка последовательно соединенных звеньев пре образуется в эквивалентное звено с передаточной функцией, рав ной произведению передаточных функций отдельных звеньев.

2. Параллельно - согласное соединение (рис.3.14.) - на вход каждого звена подается один и тот же сигнал, а выходные сигна лы - складываются. Тогда:

y =y₁ +y₂ +…- +y_п = (W₁ + W₂ + ... + W₃)y₀ = W_эквy₀

где W_экв=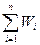

То есть цепочка звеньев, соединенных параллельно - согласно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев.

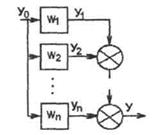
Рисунок 3.14 - Параллельно-согласное соединение звеньев САУ.

3. Параллельно - встречное соединение (рис. 3.15а) - звено охвачено положительной или отрицательной обратной связью. Участок цепи, по которому сигнал идет в противоположном на­правлении по отношению к системе в целом (то есть с выхода на вход), называется цепью обратной связи с передаточной функци­ей W_ос. При этом для отрицательной ОС:

y_n=W_n u

y₁=W_ос y

u= y₀-y₁

следовательно,

y=W_ny_0- W_ny₁ = W_ny₀- W_nW_осy

y(1+W_nW_ос)= W_ny₀

y =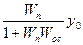

y =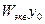

W_экв= ;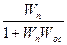

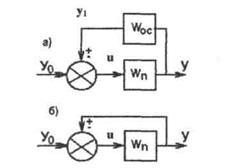
Рисунок 3.15 - Параллельно- встречное соединение звеньев.

Аналогично для положительной ОС:

W_экв= ;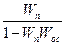

Если W_oc = 1, то обратная связь называется единичной (рис.3.156), тогда W_экв= ;.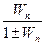

Замкнутую систему называют одноконтурной, если при ее размыкании в какой либо точке получают цепочку из последова­тельно соединенных элементов (рис.3.16а). Участок цепи, со­стоящий из последовательно соединенных звеньев, соединяющий точку приложения входного сигнала с точкой съема выходного сигнала, называется прямой цепью (рис.3.16б). Передаточная функция прямой цепи W_n=W₀W₁ W₂.

Цепь из последовательно соединенных звеньев, входящих в замкнутый контур, называют разомкнутой цепью (рис. 3.16в), пе­редаточная: функция которой W_p = W₁ W₂ W₃W₄.

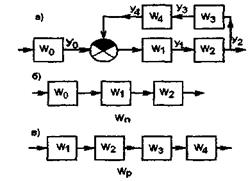
Рисунок 3.16 - Замкнутая одноконтурная система

Исходя из приведен­ных выше способов эк­вивалентного преобразо­вания структурных схем, одноконтурная система может быть представле­на одним звеном с пере­даточной функцией:

W_экв = W_п/(1 ± W_p)

- передаточная функция одноконтурной замкнутой системы с отрицательной ОС равна передаточной функции прямой цепи, поделенной на единицу плюс передаточная функция разомкнутой цепи.

Для положительной ОС в знаменателе - знак минус. Если сменить точку снятия выходного сигнала, то меняется вид пря­мой цепи. Так, если считать выходным сигнал у₁ на выходе звена W₁, то W_p = W₀W_P

Выражение для передаточной функции разомкнутой цепи не зависит от точки снятия выходного сигнала.

Замкнутые системы бывают одноконтурными и многокон­турными (рис.3.17). Чтобы найти эквивалентную передаточную функцию для данной схемы, нужно сначала осуществить преоб­разование отдельных участков.

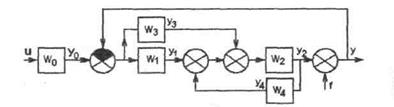
Рисунок 3.17 - Многоконтурные замкнутые системы.

Если многоконтурная система имеет перекрещивающиеся связи, то для вычисления эквивалентной передаточной функции нужны дополнительные правила. Эти правила сведены в таблицу 3.1.

Таблица 3.1- Правила структурных преобразований

Найденные с помощью правил структурных преобразований передаточные функции позволяют достаточно просто определить временные и частотные характеристики и получить качественные и количественные оценки динамики и статики САР.

Лекция 4. «Временные характеристики САУ»