Статические характеристики

Режим работы САУ, в котором управляемая величина и все промежуточные величины не изменяются во времени, называется установившимся, или статическим, режимом. Любое звено и САУ в целом в данном режиме описывается уравнениями статики вида у = F(u,f), в которых отсутствует время t. Соответствующие им графики называются статическими характеристиками. Стати­ческая характеристика звена с одним входом u может быть пред­ставлена кривой у = F(u) (рис.3.la). Если звено имеет второй вход по возмущению f, то статическая характеристика задается семейством кривых у = F(u) (рис 3.16), при различных значениях f_j, или у = F(f) при различных u_j (рис.3.1в).

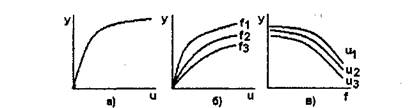
Рисунок 3.1- Статическая характеристика звена с одним входом у=F(u).

Рисунок 3.2 - Рычаг - функциональное звено системы регулирования воды в баке.

Так, примером одного из функциональных звеньев системы Регулирования воды в баке (рис. 2.10) является обычный рычаг (рис.3.2.). Уравнение статики для него имеет вид у = Ки. Его можно изобразить звеном, функцией которого является усиление (или ослабление) входного сигнала в К раз. Коэффициент К = у/и, равный отношению выходной величины к входной, называется коэффициентом усиления звена. В случае, когда входная и вы­ходная величины имеют разную природу, его называют коэффи­циентом передачи.

Статическая характеристика данного звена имеет вид отрезка прямой линии с наклоном α = arctg (L₂/L₁) = arctg(К) (рис.3.3.). Звенья с линейными статическими характеристиками называются линейными.

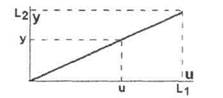
Рисунок 3.3 - Статическая характеристика рычага.

Статические характеристики реальных звеньев, как правило, нелинейны. Такие звенья называются нелинейными. Для них ха­рактерна зависимость коэффициента передачи от величины вход­ного сигнала: К = ∆у/∆и≠ const.

Например, статическая характеристика насыщенного генера­тора постоянного тока представлена на рис.3.4. Обычно нелиней­ная характеристика не может быть выражена какой-либо матема­тической зависимостью и ее приходится задавать таблично или графически.

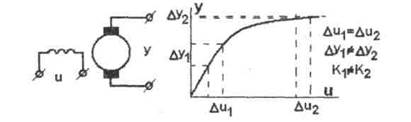
Рисунок 3.4 - Статическая характеристика насыщенного генератора постоянного тока

Зная статические характеристики отдельных звеньев (рис.3.5), можно построить статическую характеристику САУ (рис.3.6). Если все звенья САУ линейные, то САУ имеет линей­ную статическую характеристику и называется линейной. Если хотя бы одно звено нелинейное, то САУ - нелинейная.

Звенья, для которых можно задать статическую характери­стику в виде жесткой функциональной зависимости выходной величины от входной, называются статическими. Если такая связь отсутствует и каждому значению входной величины соот­ветствует множество значений выходной величины, то такое зве­но называется астатическим. Изображать его статическую харак­теристику бессмысленно.

Рисунок 3.5 - Статические характеристики отдельных звеньев САУ

Для построения статической характеристики системы по из­вестным статическим характеристикам ее звеньев по оси абсцисс, (рис. 3.6), откладываются текущие значения входного параметра u. Перпендикулярно к этой оси вверх откладывают прямые до пе­ресечения с первой характеристикой y₁=f(u). Затем от точки пере­сечения параллельно оси и проводят прямую до пересечения со второй характеристикой y₂=f(u). Далее прямую снова поворачи­вают под прямым углом вниз до пересечения с характеристикой y₃=f(u). В точке пересечения проводят прямую, параллельную оси u до пересечения с ординатами, проведенными для данного зна­чения u. Характеристика y=f(u) является искомой статической характеристикой всей САУ.

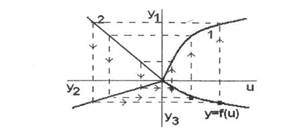
Рисунок 3.6 - К построению статической характеристики САУ.

Имея табличные характеристики звеньев для каждого значе­ния входной величины и можно получить произведение y=f(u)= y₁(u)y₂(u)y₃(u..

Примером астатического звена может служить двигатель, входной величиной которого является напряжение U, а выход­ной - угол поворота вала, величина которого при U = const может принимать любые значения. Выходная величина астатического звена даже в установившемся режиме является функцией време­ни.