Понятие частотных характеристик

В условиях реальной эксплуатации САР часто возникает не­обходимость определить реакцию на периодические сигналы, т.е. определить сигнал на выходе САР, если на один из входов пода­ется периодически сигнал гармонической формы. Решение этой задачи возможно получить путем использования частотных ха­рактеристик системы.

Зависимости, связывающие амплитуду и фазу выходного сигнала с частотой входного сигнала, называются частотными характеристиками (ЧХ). Анализ ЧХ системы с целью исследо­вания ее динамических свойств называется частотным анали­зом.

Частотные характеристики могут быть получены экспери­ментальным или аналитическим путем. При аналитическом опре­делении исходным моментом является одна из передаточных функций САР (по управлению или по возмущению).

Возможно также определение частотных характеристик ис­ходя из передаточных функций разомкнутой системы и переда­точной функции по ошибке.

Если подать на вход системы с передаточной функцией W(p) гармонический сигнал

u(t)= U_m(cost+j sinωt),

где U_m - амплитуда колебаний, ω - частота колебаний, t - время, то после завершения переходного процесса на выходе установят­ся гармонические колебания

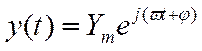
с той же частотой ω, но иными амплитудой Y_m и фазой φ, завися­щими от частоты ωвозмущающего воздействия. По ним можно судить о динамических свойствах системы.

Подставим выражения для u(t) и y(t) в уравнение динамики

(а₀р^п + а₁р^n-1 + а₂р^n-2 + ... + a_n)y = (b₀p^m + b₁p^m-1 + ... + b_m)u

Учтем, что

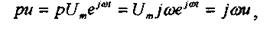
а значит

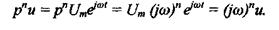
Аналогичные соотношения можно записать и для левой части уравнения. Получим:

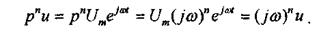
По аналогии с передаточной функцией можно записать

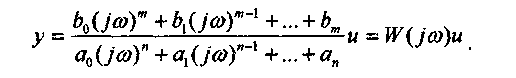
W(jω), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называ­ется частотной передаточной функцией. Легко заметить, что она может быть получена путем простой замены р на jω в выражении W(p).

W(jω) есть комплексная функция, поэтому:

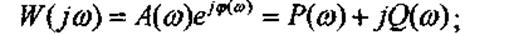
где Р(ω) - вещественная ЧХ (ВЧХ); Q(ω) - мнимая часть ЧХ (МЧХ); А(ω) - амплитудная ЧХ (АЧХ); φ(ω) - фазовая ЧХ (ФЧХ).

АЧХ дает отношение амплитуд выходного и входного сигна­лов, ФЧХ - сдвиг по фазе выходной величины относительно входной:

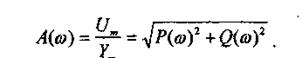
Если W(jω) изобразить вектором на комплексной плоскости, то при изменении

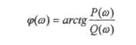
и ω от 0 до + ∞ его конец будет вычерчивать кривую, называемую годографом вектора W(jω), или амплитудно - фазовую частот­ную характеристику (АФЧХ) (рис.5.1.). Ветвь АФЧХ при изме­нении ωот - ∞ до 0 можно получить зеркальным отображением данной кривой относительно вещественной оси.

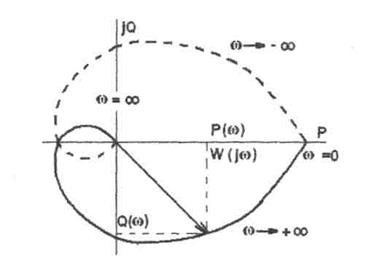
Рисунок 5.1 - Годограф вектора W(jω) (АФЧХ).

В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) (рис.5.2.): логарифмическая амплитудная ЧХ (ЛАЧХ) L(ω) и логарифмическая фазовая ЧХ (ЛФЧХ) φ(ω). Они получаются путем логарифмирования передаточной функ­ции.

По оси абсцисс откладывается частота ωв логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соот­ветствует изменение ω в 10 раз. Такой интервал называется де­кадой. Так как lg(0)=-∞, то ось ординат проводят произвольно.

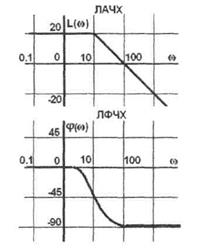
Рисунок 5.2 - Логарифмические частотные характеристики.

5.2. Частотные характеристики типовых звеньев

Зная передаточную функцию звена W(p) легко получить все его частотные характеристики. Для этого необходимо подставить в нее jω вместо р, получим АФЧХ W(jω). Затем надо выразить из нее ВЧХ Р(ω) и МЧХ Q(ω). После этого преобразуют АФЧХ в показательную форму и получают АЧХ А(ω) и ФЧХ φ(ω), а затем определяют выражение ЛАЧХ L(ω) = 20lgA(ω) (ЛФЧХ отличает­ся от ФЧХ только масштабом оси абсцисс).

5.2.1. Безынерционное звено

Передаточная функция:

W(p) = k.

АФЧХ: W(jω) =k

ВЧХ: Р(ω) = к.

МЧХ: Q(ω) = 0

АЧХ: А(ω) = к

ФЧХ: φ(ω) = 0

ЛАЧХ: L(ω) = 20lgk.

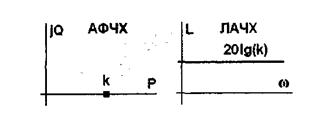
Рисунок 5.3 - АФЧХ и ЛФЧХ безынерционного звена.

Некоторые ЧХ показаны на рис.5.3. Звено пропускает все частоты одинаково с увеличением амплитуды в к раз и без сдвига по фазе.

5.2.2. Интегрирующее звено

Передаточная функция: W(p) = к/р.

Рассмотрим частный случай, когда к = 1, то есть W(p) = 1/р.

АФЧХ: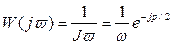

ВЧХ: Р(ω) = 0.

МЧХ: Q(ω) = -1/ ω.

АЧХ:А(ω) = 1/ ω.

ФЧХ: φ(ω) = -π/2

ЛАЧХ: L(ω) = 20lg(l/ω) = - 20lg(ω)

ЧХ показаны на рис.5.4. Все частоты звено пропускает с за­паздыванием по фазе на φ=90°. Амплитуда выходного сигнала увеличивается при уменьшении частоты и уменьшается до нуля при росте частоты (звено "заваливает" высокие частоты).

ЛАЧХ представляет собой прямую, проходящую через точку L(ω)=0 при ω=1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен – 20 дб/дек (децибел на декаду).

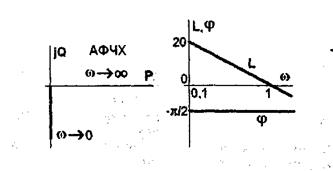
Рисунок 5.4 - Частотные характеристики интегрирующего звена.

Апериодическое звено

Для апериодического звена при к = 1 получаем следующие выражения ЧХ.

Передаточная функция

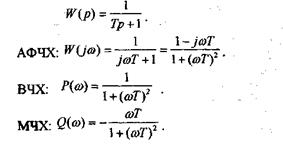
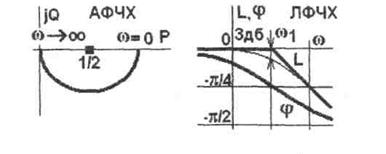
Рисунок 5.5 - Частотные характеристики для апериодического звена.

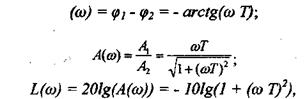
где: A₁ и А₂ - амплитуды числителя и знаменателя ЛФЧХ; φ₁ и φ₂ - аргументы числителя и знаменателя.

Частотные характеристики показаны на рис.5.5. АФЧХ есть полуокружность радиусом 1/2 с центром в точке Р= 1/2.

При построении асимптотической ЛАЧХ считают, что при (ω <ω₁ = 1/Т можно пренебречь компонентой (ωТ)² в выражении для L(ω), то есть L(ω)≈lg1= 0. При ω>ω₁ пренебрегают единицей в выражении в скобках, то есть L(ω)≈-20lg(ω).

Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота ω₁ называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при ω =ω₁

ЛФЧХ асимптотически стремится к нулю при уменьшении ω до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и к- л/2 при возрастании ω до бесконечности. Перегиб в точке ω = ω₁ при φ(ω) = -π/4. ЛФЧХ всех апериодических звень­ев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.