Неіснування ідеального алгоритму

Як уже було згадано в попередньому пункті, зображення I розглядається як безліч (послідовність) значень атрибутів пикселей. Надалі в цій лекції всі алгоритми й твердження ставляться як до зображень, так і до довільних послідовностей, елементи яких можуть приймати кінцеву кількість значень.

Твердження 13.2.1. Не існує алгоритму, що стискає без втрат будь-який набір даних.

Існує 2^N послідовностей розміру N битов 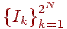(будемо розглядати біт як мінімальний носій інформації). Нехай найдеться алгоритм A такий, що 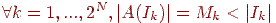, де |I| - обсяг даних (довжина послідовності). Нехай M = max M_k, тоді M < N. Існує 2¹ + 2² + ... + 2^M послідовностей довжини, меншої або рівної M. Але 2¹+2²+...+2^M = 2^{M+ 1-2} < 2^N. Протиріччя.

Із твердження треба, що має сенс розробляти алгоритми, які б ефективно стискали певний клас зображень; у той же час для цих алгоритмів завжди будуть існувати зображення, для яких вони не забезпечать стиски.