Текстури

Текстура поверхні - це деталізація її будови, що враховує мікрорельєф і особливості фарбування. По-перше, гладка поверхня може бути покрита яким-небудь візерунком, і тоді при її зображенні вирішується завдання відображення цього візерунка на проекції фрагментів поверхні (багатокутники). По-друге, поверхня може бути шорсткуватої, тому потрібні спеціальні прийоми імітації такого мікрорельєфу при зафарбовуванні.

Спочатку розглянемо методи відображення візерунків. Найчастіше візерунок задається у вигляді зразка, заданого на прямокутнику в декартовой системі координат 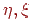у просторі текстури. Фрагмент поверхні може бути заданий у параметричному виді в тривимірної декартовой системі координат:

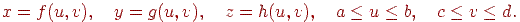
Тепер досить побудувати відображення області в просторі текстури в область параметрів поверхні

або

і тим самим кожній крапці поверхні буде відповідати крапка зразка текстури. Нехай, наприклад, поверхня являє собою один октант сфери одиничного радіуса, заданий формулами

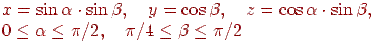
а зразок текстури заданий на квадраті 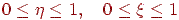. Тоді можна скористатися лінійним відображенням виду

Якщо покласти 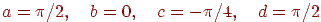, то кути зразка відобразяться в кути криволінійного чотирикутника, як це показано на мал. 12.6.

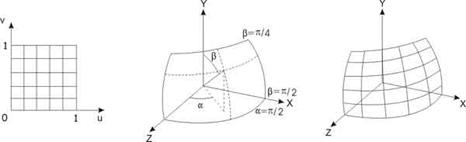
Рис. 12.5. Текстура на сферичній поверхні

Зворотне відображення має вигляд

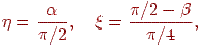
отже, вертикальні й горизонтальні лінії зразка відобразяться на окружності великого кола сфери.

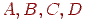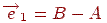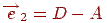Нехай тепер потрібно нанести текстуру при перспективному проектуванні довільно орієнтованої прямокутної грані. Грань задана в просторі набором своїх вершин . Побудуємо вектори й , спрямовані уздовж сторін прямокутника. Будь-яку крапку прямокутника можна єдиним образом представити у вигляді

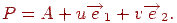
Будемо вважати, що використовується найпростіший випадок перспективного перетворення, що задається формулами

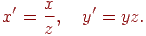
Знайдемо образ крапки P при такому перетворенні:

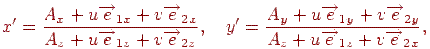
або

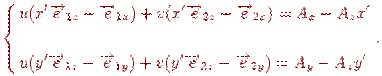
Якщо тепер розглядати ці співвідношення як систему рівнянь для знаходження параметрів 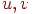, те, вирішивши її, одержимо необхідне зворотне перетворення. Для рішення можна скористатися, наприклад, правилом Крамера:

де

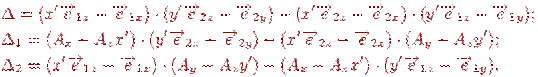
Знайдені параметри будуть визначати крапку текстури, що відповідає крапці проекції.

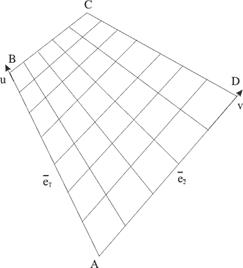
Рис. 12.6. Текстура при перспективній проекції

Можна розглянути більше загальний випадок перспективної проекції, що задається співвідношеннями

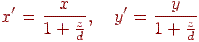
Тоді рівняння для визначення 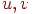небагато ускладняться:

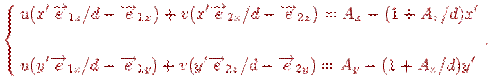
Відповідно, зміниться й рішення:

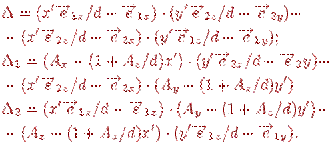
У розглянутих прикладах ми мали справу із гладкими поверхнями. Можна імітувати шорсткість шляхом вибору підходящого зразка нерегулярної текстури, але однаково зображення буде виглядати так, немов неоднорідності нанесені на гладкій поверхні. Для моделювання мікрорельєфу Дж.Млинець запропонував метод, заснований на збурюванні нормалі до поверхні.

Нехай, як і раніше, поверхня задана в параметричному виді за допомогою векторної функції 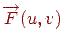. У кожній її крапці можна побудувати вектор нормалі, скориставшись частками похідними цієї функції. Відомо, що похідн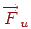і і 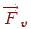являють собою вектори, що лежать у дотичної площини даної поверхні. Тоді вектор нормалі може бути отриманий як векторний добуток цих двох векторів 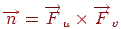. Після цього крапку поверхні можна відхилити від первісного положення в напрямку нормалі на деяку малу величину, що задається за допомогою функції збурювання :

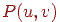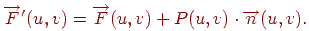
Можна показати, що нормаль до нової обуреної поверхні буде визначатися вираженням

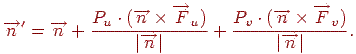
Застосовуючи в моделі висвітлення нову нормаль, можна одержати ефект шорсткості поверхні. Як функція збурювання можна використовувати довільну дифференцируемую по кожнійій зі змінних функцію.

Питання й вправи

1. Які етапи виділяються у свето-тіньовому аналізі?

2. До якого типу ставиться алгоритм Аппеля: ітеративному або рекурсивному?

3. Чи можливо використання алгоритму Аппеля для сцен з неповним затіненням?

4. Що таке тіньовий буфер? Чим він відрізняється від традиційного Z-Буфера?

5. У чому складається модифікація алгоритму Вейлера-Азертона для виконання свето-тіньового аналізу?

6. У якій моделі освітленості можна використовувати метод излучательности?

7. Чим відрізняється трасування променів у глобальній моделі освітленості від методу видалення невидимих граней?

8. Які складові інтенсивності розглядаються в методі трасування?

9. Яким образом можна використовувати двійкові дерева в алгоритмі трасування?

10. Який спосіб завдання поверхні найбільш зручний для текстурирования?

11. У чому складається ідея моделювання мікрорельєфу при нанесенні текстур?