Метод излучательности

У цій лекції вже говорилося, що освітленість поверхні визначається власним випромінюванням тіла й відбитих променів, що падають від інших тіл (джерел). Модель излучательности включає обоє ці факторів і заснована на рівняннях енергетичного балансу. При цьому виконувані розрахунки враховують тільки взаємне розташування елементів сцени й не залежать від положення спостерігача.

Представимо сцену з 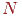елементів (ділянок поверхонь). Освітленість будемо моделювати як кількість енергії, випромінювана поверхнею. Для кожного елемента ця кількість енергії складається із власної енергії 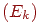й відбитої частки енергії, отриманої від інших об'єктів. Передбачається, що для кожної пари елементів з номерами 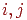можна визначити, яка частка енергії одного попадає на іншій 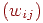. Нехай 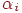- коефіцієнт відбиття енергії 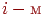елементом. Тоді повна енергія, випромінювана цим елементом, буде визначатися рівнянням .

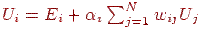Таким чином, ми одержуємо систему рівнянь для знаходження значень 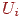, що у матричному виді виглядає в такий спосіб:

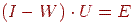
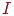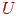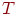де - одинична матриця, і - вектори випромінюваної й власної енергій, а матриця 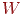складається з елементів 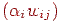. Оскільки частина випромінювання елемента може не попадати ні на один із що залишилися, те

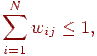
а ця умова в сполученні з тим, що 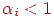(відбиття не є повним), приводить до того, що матриця системи має так звану діагональну перевагу, тобто діагональний елемент по абсолютній величині більше, ніж сума інших елементів рядка. У такому випадку система рівнянь має рішення, яке можна знайти за допомогою чисельних методів.

Отже, кроки алгоритму зображення сцени зводяться до наступним:

1. Сцена розбивається на окремі ділянки, для кожного з яких визначаються значення .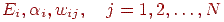

2. Перебувають значення 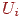для кожного із трьох основних компонентів кольору.

3. Для обраної крапки спостереження стоїться проекція з видаленням невидимих граней і здійснюється зафарбовування, що використовує значення 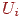для завдання інтенсивності. При цьому можуть використовуватися які-небудь алгоритми, що дозволяють згладити зображення.

Складним моментом у моделі излучательности є розрахунок коефіцієнтів .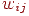

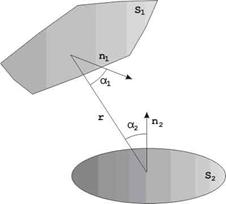
Рис. 12.2. Два елементи сцени

Розглянемо один приклад. Нехай є два елементи сцен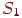и й 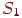(мал. 12.2). Оскільки використовується дифузійна модель висвітлення, то частка енергії малої ділянки 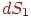з нормаллю 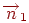, випромінювана під кутом 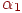до цієї нормалі, пропорційна косинусу кута. Отже, у напрямку елементарної ділянки 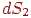йде частка енергії, пропорційна косинусу кута між 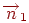і відрізком, що з'єднує ці ділянки. Відповідно, одержувана другою ділянкою частка цієї енергії буде пропорційна косинусу кута між нормаллю 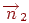й цим же відрізком. Отже, частка енергії, одержувана елементом 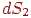від елемента , 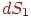- 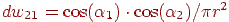, де 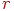- відстань між елементами. Крім того, необхідно врахувати, що випромінювана елементарною ділянкою енергія рівномірно розподілена в усіх напрямках. І, нарешті, у кожній сцені одні об'єкти можуть частково екранувати інші, тому треба ввести коефіцієнт, що визначає ступінь видимості об'єкта з позиції іншого. Далі отримане вираження інтегрується по 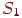й 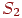, що також може бути складним завданням.

Звідси видно, наскільки трудомісткої може виявитися процедура обчислення коефіцієнтів 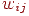. Тому, як правило, використовуються наближені методи їхнього обчислення. Зокрема, можна розглядати поверхні об'єктів як багатогранники, тоді елементами сцени будуть плоскі багатокутники, для яких формули трохи спрощуються.