Рівняння прямій і площині
Рівняння прямої на площині в декартовії системі координат можна задати рівнянням виду
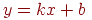
для випадку, коли пряма не паралельна осі OY, і рівнянням
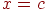
для вертикальної прямої. Але пряма може бути також задана й іншим способом. Досить указати вектор напрямку цій прямій 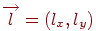 і якій-небудь крапці
і якій-небудь крапці 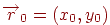 , що лежить на цій прямій. При цьому крапки, що лежать на прямій, можуть бути задані з використанням векторних операцій у вигляді так званого параметричного рівняння прямій
, що лежить на цій прямій. При цьому крапки, що лежать на прямій, можуть бути задані з використанням векторних операцій у вигляді так званого параметричного рівняння прямій

у якому параметр t пробігає всі значення числової прямої. Координати крапки, що відповідає деякому значенню цього параметра, визначаються співвідношеннями

| (4.4) |
Пряму в просторі теж можна задавати параметричним рівнянням, що дуже легко одержати з попереднім простим переходом від двовимірних векторів до тривимірного. Нехай 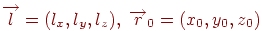 . Тоді це рівняння буде визначати пряму в просторі, а координати крапок цій прямій будуть визначатися формулами
. Тоді це рівняння буде визначати пряму в просторі, а координати крапок цій прямій будуть визначатися формулами
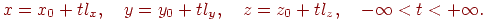
| (4.5) |
Як відомо з елементарної геометрії, через будь-які три крапки в просторі проходить площина. З іншого боку, через кожну крапку площини можна провести єдину пряму, перпендикулярну даної площини. При цьому всі ці прямі будуть паралельні один одному, а виходить, вони мають загальний вектор напрямку. Цей вектор будемо називати нормаллю до площини. Якщо довжина вектора дорівнює одиниці, ми будемо називати його одиничною нормаллю. У комп'ютерній графіці часто доводиться вирішувати завдання побудови нормалі до деякої площини, заданої трьома крапками, а також завдання перетинання прямій із площиною й двох площин.
Площина в просторі можна задати, указавши вектор нормалі до неї і яку-небудь крапку, що належить даної площини. Нехай 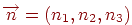 - вектор одиничної нормалі, а
- вектор одиничної нормалі, а  - деяка крапка на площині. Тоді для будь-якої крапки
- деяка крапка на площині. Тоді для будь-якої крапки 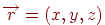 , що лежить на площини, вектор
, що лежить на площини, вектор  буде ортогонален вектору нормалі, а отже, виконується рівність
буде ортогонален вектору нормалі, а отже, виконується рівність
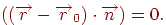
Розкриваючи це вираження в координатному виді, одержуємо

Тепер перепишемо це рівняння у вигляді
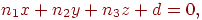
| (4.6) |
де 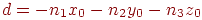 . Це рівняння називається канонічним рівнянням площини. При цьому зовсім ясно, що якщо все це рівняння помножити на який-небудь відмінний від нуля множник, то воно буде описувати ту ж саму площину, тобто коефіцієнти
. Це рівняння називається канонічним рівнянням площини. При цьому зовсім ясно, що якщо все це рівняння помножити на який-небудь відмінний від нуля множник, то воно буде описувати ту ж саму площину, тобто коефіцієнти 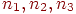 для кожної площини задаються з точністю до довільного ненульового множника. Але якщо при цьому вектор
для кожної площини задаються з точністю до довільного ненульового множника. Але якщо при цьому вектор 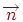 має одиничну довжину, то
має одиничну довжину, то 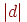 задає відстань від початку координат до даної площини.
задає відстань від початку координат до даної площини.
В алгоритмах комп'ютерної графіки досить часто доводиться зіштовхуватися із завданням побудови площини, що проходить через три задані крапки. Нехай три крапки 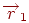 ,
, 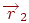 і
і 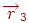 , що не лежать на одній прямій, мають координатами
, що не лежать на одній прямій, мають координатами 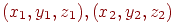 й
й 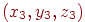 . Для канонічного рівняння необхідно побудувати нормаль до площини, що легко можна здійснити, використовуючи операцію векторного добутку. Оскільки вектори
. Для канонічного рівняння необхідно побудувати нормаль до площини, що легко можна здійснити, використовуючи операцію векторного добутку. Оскільки вектори 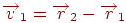 й
й  лежать у шуканій площині, то вектор
лежать у шуканій площині, то вектор 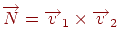 буде ортогонален цієї площини. Нехай
буде ортогонален цієї площини. Нехай 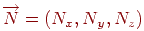 , тоді рівняння площини буде мати вигляд
, тоді рівняння площини буде мати вигляд
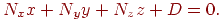
Залишається визначити значення  . Тому що крапка
. Тому що крапка 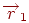 належить цій площині, те її координати повинні задовольняти отриманому рівнянню. Підставимо їх у рівняння й одержимо
належить цій площині, те її координати повинні задовольняти отриманому рівнянню. Підставимо їх у рівняння й одержимо
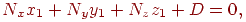
отже

і після підстановки остаточно одержимо:
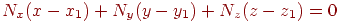
| (4.7) |
У більшості алгоритмів, що використовують площини, досить знати нормаль до неї і яку-небудь крапку, що належить площини. Очевидно, що за аналогією можна вивести канонічні рівняння прямої на площині, якщо задано нормаль до неї й приналежній прямій крапка.
Дата добавления: 2015-04-03; просмотров: 1259;
