Перетинання лучачи із площиною й сферою
Пряма на площині й у просторі є нескінченною в обидва боки. Променем називається напівпряма, тобто безліч всіх крапок прямій, що лежать по одну сторону від заданої її крапки, називаної початком лучачи. Промінь будемо задавати в параметричному виді, як це було описано в одному з попередніх розділів. Нехай 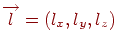 - напрямний вектор прямій, а
- напрямний вектор прямій, а  - початкова крапка. Тоді координати крапок лучачи будуть визначатися формулами
- початкова крапка. Тоді координати крапок лучачи будуть визначатися формулами
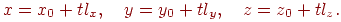
| (4.8) |
Будемо вважати, що напрямний вектор одиничний, тобто 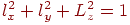 .
.
Спочатку розглянемо завдання про знаходження крапки перетинання лучачи із площиною, заданої канонічними рівнянням
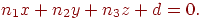
| (4.9) |
Вектор нормалі 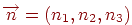 теж будемо вважати одиничним. Спочатку треба визначити значення параметра t, при якому промінь перетинає площина. Для цього підставимо координати з формули (4.8) у рівняння (4.9) і одержимо
теж будемо вважати одиничним. Спочатку треба визначити значення параметра t, при якому промінь перетинає площина. Для цього підставимо координати з формули (4.8) у рівняння (4.9) і одержимо
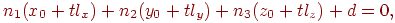
звідки легко визначити, що промінь перетинає площина в крапці зі значенням
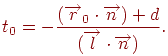
Очевидно, що така крапка існує тільки за умови 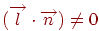 . У свою чергу, ця величина звертається в нуль тільки у випадку, коли вектори
. У свою чергу, ця величина звертається в нуль тільки у випадку, коли вектори 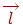 й
й 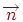 ортогональні один одному.
ортогональні один одному.
Нехай тепер нам задана сфера із центром у крапці  й радіусом
й радіусом 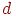 . Тоді рівняння сфери буде мати вигляд
. Тоді рівняння сфери буде мати вигляд
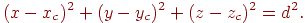
Підставивши сюди координати лучачи з рівняння (4.9), одержимо, що параметр, при якому промінь перетинає сферу, повинен задовольняти квадратному рівнянню
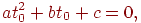
де 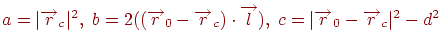 . Визначимо корінь цього рівняння. Якщо дискримінант
. Визначимо корінь цього рівняння. Якщо дискримінант 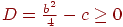 , то корінь існують. Їх може бути або два
, то корінь існують. Їх може бути або два  , або один
, або один 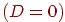 . У першому випадку маємо дві крапки перетинання, у другому - одну (промінь стосується сфери). Відповідні значення параметра визначаються співвідношенням
. У першому випадку маємо дві крапки перетинання, у другому - одну (промінь стосується сфери). Відповідні значення параметра визначаються співвідношенням
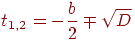
Дата добавления: 2015-04-03; просмотров: 1070;
